题目内容
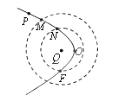
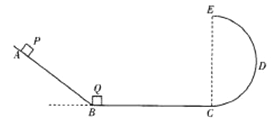
【题目】如图所示,光滑斜面AB与一段粗糙的水平轨道BC通过光滑的圆弧平滑连接,水平轨道的右端与半径为R的光滑半圆弧轨道CDE相切。两质量相同的小物块P和Q分别置于斜面某一高度处和水平轨道的左端B点。现由静止释放P物块,当其滑至斜面底端通过光滑圆弧段之后与小物块Q发生碰撞,碰撞之后粘在一起沿水平轨道向右运动。已知两物块与水平轨道BC之间的动摩擦因数均为μ=0.5,BC长度为3R,重力加速度为g,两小物块均可视为质点。若两物块能到达圆弧轨道的最高点E,求小物块P释放点的最小高度h。
【答案】16R
【解析】
沿光滑斜面下滑由满足机械能守恒求速度,碰撞过程由动量守恒定律求碰后速度,由圆周运动的绳—球模型抓住最高的临界条件求高度.
设两小物块质量均为m,小物块P的释放点距离水平地面的高度为h.
在小物块P下滑过程中满足机械能守恒,则有![]()
设碰撞之后共同速度为v,两小物块碰撞过程中满足动量守恒定律![]()
联立解得:![]()
如释放点高度h1,恰使得两小物块运动至E点,则由动能定理可得:
![]()
其中![]()
小物块在E点满足![]()
联立解得:![]()

练习册系列答案
相关题目