题目内容
【题目】如图甲所示，半径为R=0.45 m的光滑圆弧轨道固定在竖直平面内，B点为轨道最低点，在光滑水平面上紧挨B点有一静止的平板车，其质量M=5 kg，长度L=0.5 m，车的上表面与B点等高，可视为质点的物块从圆弧轨道最高点A由静止释放，其质量m=1 kg，g取10 m/s2.
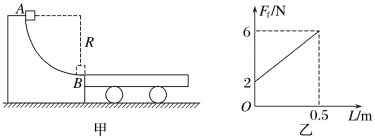
(1)求物块滑到B点时对轨道压力的大小；
(2)若平板车上表面粗糙，物块最终没有滑离平板车，求物块最终速度的大小；
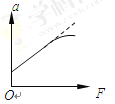
(3)若将平板车固定且在上表面铺上一种动摩擦因数逐渐增大的特殊材料，物块在平板车上向右滑动时，所受摩擦力Ff随它距B点位移L的变化关系如图乙所示，物块最终滑离了平板车，求物块滑离平板车时的速度大小．
【答案】(1)30N(2)0.5m/s(3)
m/s
【解析】
解：(1)物块从圆弧轨道
点滑到
点的过程中机械能守恒：
解得：
在点由牛顿第二定律得：
解得：
则物块滑到点时对轨道的压力：
(2)物块滑上平板车后，系统的动量守恒，则有：
共
解得：
共
(3)物块在平板车上滑行时克服摩擦力做的功为
图线与横轴所围的面积，则克服摩擦力做功为：
物块在平板车上滑动的过程中，由动能定理得：
解得：
练习册系列答案
名校课堂系列答案
相关题目
