题目内容
(1)物块两次滑过传送带的过程中,摩擦力对物块做功的绝对值之比为多少?
(2)当传送带的转动速度在某一范围内时,物块通过传送带的时间达到最短.求这一最短时间.
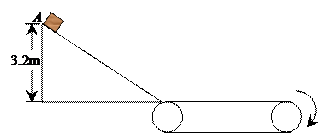
(1)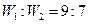 (2)1s
(2)1s
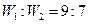 (2)1s
(2)1s(1)根据机械能守恒定律(或动能定理)计算出小物块冲上传送带时的速度:
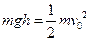 ……………………………(1分)
……………………………(1分)
传送带静止时,滑动摩擦力全程都对物块做负功,设摩擦力做功为W1:
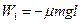 = -18J……………………………(1分)
= -18J……………………………(1分)
又小物块运动到传送带末端时,速度为vt:
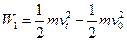 ……………………………(2分)
……………………………(2分)
解得:vt=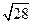 m/s <6m/s ……………(1分)
m/s <6m/s ……………(1分)
所以,当传送带以6m/s速度转动时,物块速度减小到6m/s,就不再减小,此后无摩擦力做功。设此过程摩擦力做功为W2,则:
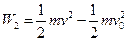 ,末速度v=6m/s,……………………………(2分)
,末速度v=6m/s,……………………………(2分)
解得:W2= -14J……………………………(1分)
所以,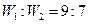 ……………………………(1分)
……………………………(1分)
(2)无论传送带转动多快,小物块仅在摩擦力作用下,加速度不会超过:
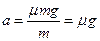 ……………………………(1分)
……………………………(1分)
要使时间最短,小物块应该全程加速。当其相对于地的位移等于传送带长时:
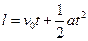 ……………………………(2分)
……………………………(2分)
解得:最短时间t=1s。……………………………(2分)
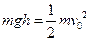 ……………………………(1分)
……………………………(1分)传送带静止时,滑动摩擦力全程都对物块做负功,设摩擦力做功为W1:
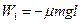 = -18J……………………………(1分)
= -18J……………………………(1分)又小物块运动到传送带末端时,速度为vt:
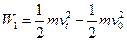 ……………………………(2分)
……………………………(2分)解得:vt=
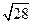 m/s <6m/s ……………(1分)
m/s <6m/s ……………(1分)所以,当传送带以6m/s速度转动时,物块速度减小到6m/s,就不再减小,此后无摩擦力做功。设此过程摩擦力做功为W2,则:
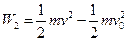 ,末速度v=6m/s,……………………………(2分)
,末速度v=6m/s,……………………………(2分)解得:W2= -14J……………………………(1分)
所以,
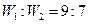 ……………………………(1分)
……………………………(1分)(2)无论传送带转动多快,小物块仅在摩擦力作用下,加速度不会超过:
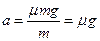 ……………………………(1分)
……………………………(1分)要使时间最短,小物块应该全程加速。当其相对于地的位移等于传送带长时:
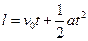 ……………………………(2分)
……………………………(2分)解得:最短时间t=1s。……………………………(2分)

练习册系列答案
相关题目
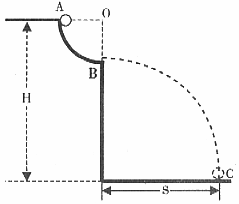
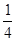 圆弧形轨道,圆弧半径为R,O为圆心,OA水平,CD是一段水平光滑轨道.一根长为2R、粗细均匀的细棒,开始时正好搁在圆弧轨道两个端点上,现由静止释放细棒,则此棒最后在水平轨道上滑行的速度为__________.
圆弧形轨道,圆弧半径为R,O为圆心,OA水平,CD是一段水平光滑轨道.一根长为2R、粗细均匀的细棒,开始时正好搁在圆弧轨道两个端点上,现由静止释放细棒,则此棒最后在水平轨道上滑行的速度为__________.




 。已知小球a质量为m,重力加速度为g。
。已知小球a质量为m,重力加速度为g。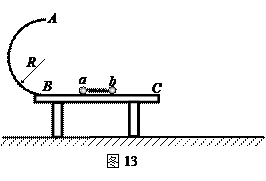 (3)释放小球前弹簧具有的弹性势能。
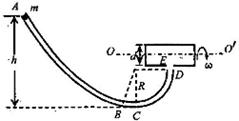
(3)释放小球前弹簧具有的弹性势能。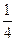 圆弧,AC的竖直高度差h=0.45m。在紧靠管道出口D处有一水平放置且绕其水平中心轴
圆弧,AC的竖直高度差h=0.45m。在紧靠管道出口D处有一水平放置且绕其水平中心轴 匀速旋转的圆筒,圆筒直径d=0.15m,桶上开有小孔E。现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒。不计空气阻力,取
匀速旋转的圆筒,圆筒直径d=0.15m,桶上开有小孔E。现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒。不计空气阻力,取 。求:
。求: