题目内容
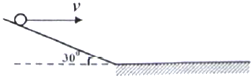
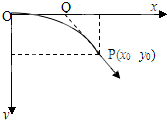
如图所示,将小球从坐标原点沿水平轴ox抛出,经一段时间到达P点,其坐标为(x0,y0).作小球轨迹在P点的切线并反向延长与Ox轴相交于Q点,则Q点的横坐标为( )
A.
| B.
| C.
| D.
|

∠xQP为P点速度的偏向角,设∠xQP=θ,设∠xOp=α,Q点的横坐标为x,小球的初速度为v0,
根据平抛运动的规律,小球经过P点时竖直分速度为:vy=gt
则有:tanθ=
=
而tanα=
=
=
即:tanθ=2tanα,
得:
=2
,
得:x=
x0;故C正确.
故选:C.
根据平抛运动的规律,小球经过P点时竖直分速度为:vy=gt
则有:tanθ=
| vy |
| v0 |
| gt |
| v0 |
而tanα=
| y0 |
| x0 |
| ||
| v0t |
| gt |
| 2v0 |
即:tanθ=2tanα,
得:
| y0 |
| x0-x |
| y0 |
| x0 |
得:x=
| 1 |
| 2 |
故选:C.

练习册系列答案
相关题目