题目内容
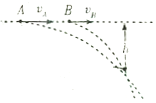
【题目】如图所示,将A.B两个小球从同一水平线上相距为L的两个位置分別以速度vA,,vB,同时水平抛出,不计空气阻力,当两球在空中的下落高度为h时,两球相遇。如果仅将两球水平抛出的速度都变为原来2倍,则两球在空中相遇时下落的高度h'为
A. h B. ![]() C.
C. ![]() h D.
h D. ![]() h
h
【答案】D
【解析】
平抛运动在水平方向上做匀速直线运动,抓住两球的水平位移不变,结合初速度的变化得出两球从抛出到相遇经过的时间,再由竖直分位移公式分析两球相遇点的位置.
两球同时抛出,竖直方向上做自由落体运动,相等时间内下降的高度相同,始终在同一水平面上,根据L=vAt-vBt知,L不变,当两球的抛出速度都变为原来的2倍,则两球从抛出到相遇经过的时间为t/2,根据h=![]() gt2,知两球下落的高度是
gt2,知两球下落的高度是![]() h,则两球在空中相遇时下落的高度h'为
h,则两球在空中相遇时下落的高度h'为![]() h.故D正确,ABC错误。故选D。
h.故D正确,ABC错误。故选D。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目