题目内容

4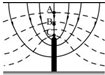．如图所示，实线为电场线，虚线为等势面，且AB=BC，电场中的A、B、C三点的场强分别为EA、EB、EC，电势分别为φA、φB、φC，AB、BC间的电势差分别为UAB、UBC，则下列关系中不正确的是（　　）
A．φA＞φB＞φCB．EC＞EB＞EAC．UAB＜UBCD．UAB＞UBC

分析 电场线密的地方电场的强度大，电场线疏的地方电场的强度小；由电场线的疏密分析场强的大小．沿电场线电势降低，根据公式U=Ed，分析电势差的大小．

解答 解：沿着电场方向电势逐渐降低，故φA＞φB＞φC；
根据电场线密的地方电场强度大，电场线稀的地方电场强度小，故EC＞EB＞EA；
由电场线的分布情况，可知AB间场强小于BC间场强，由公式U=Ed知UAB＜UBC ．故ABC正确，D不正确．
本题选不正确的，故选：

点评 本题考查了如何根据电场线的分布判断电场强度大小以及电势高低，对于非匀强电场，可根据公式U=Ed定性分析电势差的关系．

练习册系列答案
相关题目
9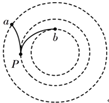．图中虚线是某电场中的一簇等势线．两个带电粒子从P点均沿等势线的切线方向射入电场，粒子运动的部分轨迹如图中实线所示．若粒子仅受电场力的作用，下列说法中正确的是（　　）
A．粒子从P运动到b的过程中，动能减小
B．a、b两点的电势关系Ua＜Ub
C．粒子从P运动到a的过程中，电势能增大
D．a、b两点的电场强度大小关系Ea＜Eb
15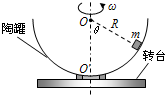．如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合．转台以一定角速度ω匀速转动．一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与OO′之间的夹角θ为53°，物块与陶瓷间的动摩擦因数为0.5，重力加速度大小为g，sin53°=0.8，cos53°=0.6．则（　　）
A．当小物块受的摩擦力为零时，小物块受重力、支持力和向心力作用
B．随着角速度ω的增大，小物块受的摩擦力逐渐增大
C．使小物块不下滑的最小角速度为ω=$\sqrt{\frac{5g}{6R}}$
D．当角速度ω=$\sqrt{\frac{5g}{3R}}$时小物块受到的摩擦力为零
12．雨滴从高空由静止下落，由于空气阻力作用，其加速度逐渐减小，直到为零，在此过程中雨滴的运动情况是（　　）
A．速度不断减小，加速度为零时，速度为零
B．速度不断增大，加速度为零时，速度最大
C．速度一直保持不变
D．位移逐渐增大，当加速度减小为零时，位移达到最大
19．假设地球可视为质量均匀分布的球体，已知一颗人造地球卫星绕地球做匀速圆周运动的半径为R，周期为T；地球的半径为R0，自转周期为T0．则地球表面赤道处的重力加速度大小与两极处重力加速度大小的比值为（　　）
A．$\frac{{R_0^3{T^2}}}{{{R^3}T_0^2}}$B．$\frac{{{R^3}T_0^2}}{{R_0^3{T^2}}}$
C．$1-\frac{{R_0^3{T^2}}}{{{R^3}T_0^2}}$D．$1-\frac{{{R^3}T_0^2}}{{R_0^3{T^2}}}$
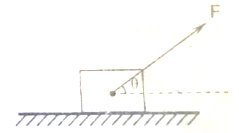9．如图所示，一物块在与水平方向成37°斜向上拉力作用下做匀速直线运动，拉力大小为15N，物块的重力为20N，试求：物块受到的摩擦力和水平面的支持力．
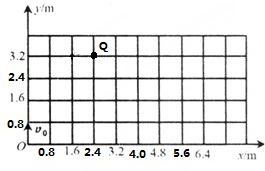16．如图所示，在竖直平面内建立xOy直角坐标系，Oy表示竖直向上的方向．已知该平面内存在沿x轴负方向的区域足够大的匀强电场，现将一个带电量为q=+2.5×10-4C、质量为m=0.05kg的小球从坐标原点O沿y轴正方向竖直向上抛出，它到达的最高点位置为图中的Q点，不计空气阻力，g取10m/s2．求：
（1）匀强电场的电场强度大小；
（2）小球从0点抛出到落回x轴的过程中电势能的改变量；
（3）小球在上述过程中速度的最小值．
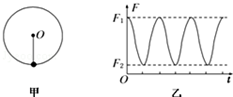13．一宇航员到达半径为R、密度均匀的某星球表面，做如下实验：用不可伸长的轻绳栓一质量为m的小球，上端固定在O点，如图甲所示，在最低点给小球某一初速度，使其绕O点在竖直平面内做圆周运动，测得绳的拉力F的大小随时间t的变化规律如图乙所示，△F=F1-F2，设R、m、引力常量G、△F均为已知量，忽略各种阻力，求：
（1）该星球的质量；
（2）若在该星球上发射一颗卫星，发射速度至少为多大？
14．如图所示，电容器上标有“400V 2.2μF”的字样，下列说法正确的是（　　）
A．该电容器两端电压是400V时，电容为2.2μF
B．该电容器的带电量是28.8×10-4C
C．该电容器的工作电压是400V
D．该电容器的击穿电压是400V

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网