题目内容
【题目】如图所示,足够长的水平传送带沿顺时针方向以v0=2m/s的速度匀速转动,A、B两个完全相同的小物块从M点和N点同时以v=4m/s的初速度相向运动。已知小物块A、B在传送带上运动的过程中恰好不会发生碰撞,小物块A、B均可视为质点且与传送带间的动摩擦因数μ=0.4,重力加速度g取10 m/s2。求:
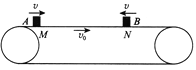
(1)两个小物块相对传送带运动时间的差值。
(2)M点和N点之间的距离。
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)由牛顿第二定律μmg=ma
可知两个小物块的加速度均为a=μg=4m/s2
小物块A向右减速至与传送带共速的过程中所需时间![]()
解得tA=0.5s
小物块B向左减速至0再反向加速至与传送带共速的过程所需的时间![]()
故两个小物块相对传送带运动的时间差为tB-tA=1s
(2)两小物块恰好不发生碰撞,应该在小物块B与传送带共速时恰好到达同一点,在tB=1.5s内小物块A向右运动的位移![]()
解得xA=3.5m
在tB=1.5s内小物块B向左运动的位移![]() 解得xB=1.5m
解得xB=1.5m
M点和N点的距离为xA+xB=5m

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目