Question

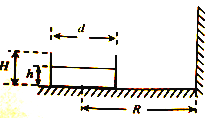
【题目】直径d=1.40m，高H=0.70m的不透明圆桶（桶壁厚度不计），桶内盛有高h=0.40m某种透明液体，桶位于半径R=2.70m圆柱形墙房屋的正中央，如图所示。在桶底中心处放一点光源，能照亮高出地面2.2m以上的墙壁。求：

①透明液体的折射率。

②桶内装满折射率为1.5的透明液体时，未被照亮墙壁的高度。

Answer 1

【答案】(1) (2) 0.70m

【解析】本题考查光的折射和全反射。

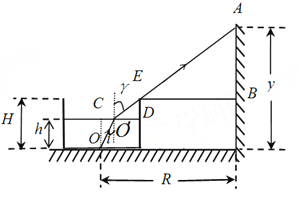
①设O点发出的光经过液面上O′点照亮墙上A点．

与相似， 得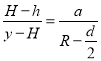： ；其中a为O′D的长度

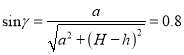
折射定律：

解得：

②设装满液体时光线由液体内射向空气的最大入射角为θ，由图的几何关系得：

，即最大入射角θ＝45°

而

也就是C＜45°，说明能发生全反射。

因此，未照亮的墙壁高度为H＝0.70m