题目内容
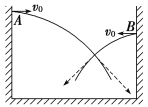
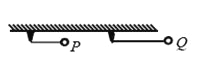
【题目】如图所示,可视为质点的小球P和Q用不可伸长的轻绳悬挂在天花板上,P球的质量大于Q球的质量,悬挂P球的绳比悬挂Q球的绳短。将两球拉起,使两绳均被水平拉直。将两球由静止释放,在各自轨迹的最低点( )
A. P球的速度一定大于Q球的速度
B. P球的动能一定小于Q球的动能
C. P球的向心加速度等于Q球的向心加速度
D. P球所受绳的拉力大于Q球所受绳的拉力
【答案】CD
【解析】
从静止释放至最低点,由机械能守恒列式,得到最低点的速度表达式;在最低点由牛顿第二定律可得绳子的拉力和向心加速度表达式,再比较它们的大小。
对任意一球,设绳子长度为L.小球从静止释放至最低点,由机械能守恒得:![]() ,解得:
,解得:![]() ,可知通过最低点时,P球的速度一定小于Q球的速度,故A错误;到达最低点时的动能
,可知通过最低点时,P球的速度一定小于Q球的速度,故A错误;到达最低点时的动能![]() ,由于P球的质量大于Q球的质量,而悬挂P球的绳子较短,所以不能判断动能的大小,故B错误;在最低点小球的向心加速度
,由于P球的质量大于Q球的质量,而悬挂P球的绳子较短,所以不能判断动能的大小,故B错误;在最低点小球的向心加速度![]() ,与L无关,所以P球的向心加速度一定等于Q球的向心加速度,故C正确;在最低点,由拉力和重力的合力提供向心力,由牛顿第二定律得:
,与L无关,所以P球的向心加速度一定等于Q球的向心加速度,故C正确;在最低点,由拉力和重力的合力提供向心力,由牛顿第二定律得:![]() ,解得:F=3mg,与L无关,与m成正比,所以P球所受绳的拉力一定大于Q球所受绳的拉力,故D正确。所以CD正确,AB错误。
,解得:F=3mg,与L无关,与m成正比,所以P球所受绳的拉力一定大于Q球所受绳的拉力,故D正确。所以CD正确,AB错误。

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目