题目内容
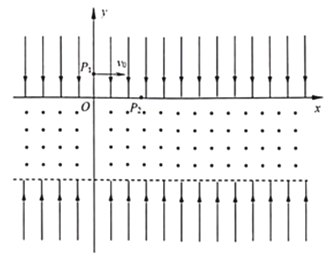
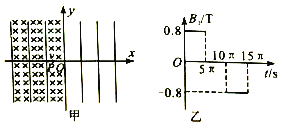
【题目】如图甲所示，在xOy平面内有足够大的匀强电场E，在y轴左侧平面内有足够大的磁场，磁感应强度B1随时间t变化的规律如图乙所示，选定磁场垂直纸面向里为正方向。在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场，分布在一个半径为r=0.3m的圆形区域(图中未画出)且圆的左侧与y轴相切，磁感应强度B2=0.8T，t=0时刻，一质量m=8×10－4kg、电荷量q=+2×10－4C的微粒从x轴上xp=－0.8m处的P点以速度v=0.12m/s向x轴正方向入射。已知该带电微粒在电磁场区域做匀速圆周运动。(g取10m/s2)
(1)求电场强度。
(2)若磁场15πs后消失，求微粒在第二象限运动过程中离x轴的最大距离；
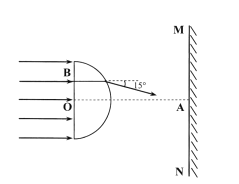
(3)若微粒穿过y轴右侧圆形磁场时速度方向的偏转角最大，求此圆形磁场的圆心坐标(x，y)。
【答案】(1) 
，方向竖直向上 (2) 
(3)
【解析】
(1)因为微粒射入电磁场后做匀速圆周运动受到的电场力和重力大小相等，则：
解得：，方向竖直向上
(2)由牛顿第二定律有：
所以
从图乙可知在
内微粒做匀速圆周运动，在
内微粒向左做匀速直线运动．在
内微粒又做匀速圆周运动，在
内微粒向右做匀速直线运动，之后穿过y轴．
离x轴的最大距离
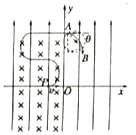
(3)如图，微粒穿过圆形磁场要求偏转角最大，入射点A与出射点B的连线必须为磁场圆的直径．
由牛顿第二定律，有
所以
所以最大偏转角为60°
所以圆心坐标
即磁场的圆心坐标为．
练习册系列答案
黄冈创优卷系列答案
相关题目
