题目内容
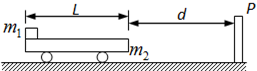 如图所示,质量m2=0.3kg的小车静止在光滑的水平面上,距车的右端d=
如图所示,质量m2=0.3kg的小车静止在光滑的水平面上,距车的右端d=| 1 | 6 |
(1)即将与挡板P相撞时小车的速度;
(2)小车长L;
(3)若小车右端与挡板P之间的距离d可调,求出能让小物块刚好在车面右端保持相对静止d的所有可能取值.
分析:(1)小车与墙壁碰撞之前,对小车,根据动能定理列式求出小车的速度;假设物块与小车碰前达到共速,小车与墙壁碰撞后,原速率反弹,之后小车与物块组成的系统动量守恒,列式求出最后两者共同的速度,作出判断,得到即将与挡板P相撞时小车的速度;
(2)小车与小车即将与挡板碰撞时,由系统的动量守恒列式求出物块的速度.小车与挡板碰后至小车与滑块再次相对静止的过程中,小车与滑块为系统动量守恒,列式求出共同速度.再根据能量守恒求解小车的长度L;
(3)小车与挡板即将发生第n次碰撞之前,小车与物块的动量大小相等,在小车与挡板第n次碰撞之后,由动量守恒可确定两者相对静止时,整体共同速度为零,系统末动能为零.这样的条件下物块相对小车静止在另外一端.运用牛顿第二定律、运动学公式和动量守恒结合分过程求解.
(2)小车与小车即将与挡板碰撞时,由系统的动量守恒列式求出物块的速度.小车与挡板碰后至小车与滑块再次相对静止的过程中,小车与滑块为系统动量守恒,列式求出共同速度.再根据能量守恒求解小车的长度L;
(3)小车与挡板即将发生第n次碰撞之前,小车与物块的动量大小相等,在小车与挡板第n次碰撞之后,由动量守恒可确定两者相对静止时,整体共同速度为零,系统末动能为零.这样的条件下物块相对小车静止在另外一端.运用牛顿第二定律、运动学公式和动量守恒结合分过程求解.
解答:解:(1)小车与墙壁碰撞之前,设速度为v1,
对小车据动能定理有:μm1gd=
m2v12-0
解得:v1=
m/s
若碰前达到共速,据动量守恒有:
m1v0=(m1+m2)v共
v共=
=0.8(m/s)
因为 v1=
m/s<v共
小车与墙壁碰撞之前速度为 v1=
m/s
(2)小车即将与挡板碰撞时,设物体的速度为v2 .
m1v0=m1v2+m2v1
v2=1m/s
小车与挡板碰后至小车与滑块再次相对静止的过程中,小车与滑块为系统动量守恒,设共速为v
m1v2-m2v1=(m1+m2)v
解得:v=0
因小车与挡板碰撞时无机械能损失,据能量转化与守恒有
μm1gL=
m1
解得:L=1m
(3)若小车与挡板即将发生第n次碰撞之前,小车与物块的动量大小相等,则在小车与挡板第n次碰撞之后,据动量守恒可确定两者相对静止时,整体共同速度为零,系统末动能为零.这样的条件下物块相对小车静止在另外一端.
令小车运动的加速度,据牛顿第二定律有:μm1g=m2a1
解得:a1=
(m/s2)
小车由静止开始匀加速至与挡板发生第一次碰撞之前,用时为t0
d=
a1
此时小车的速度 v=a1t0
至小车即将与挡板发生第n次碰撞之前,用时t=(2n-1)t0
此时,物块速度为 v′,v′=v0-a2t
且 m1v=m2v′
代入数据联解可得:t0=
d=
(m) (n=1,2,3…)
答:(1)即将与挡板P相撞时小车的速度为
m/s;
(2)小车长L为1m;
(3)能让小物块刚好在车面右端保持相对静止d的所有可能取值为 d=
(m) (n=1,2,3…).
对小车据动能定理有:μm1gd=
| 1 |
| 2 |
解得:v1=
| 2 |
| 3 |
若碰前达到共速,据动量守恒有:
m1v0=(m1+m2)v共
v共=
| m1v0 |
| m1+m2 |
因为 v1=
| 2 |
| 3 |
小车与墙壁碰撞之前速度为 v1=
| 2 |
| 3 |
(2)小车即将与挡板碰撞时,设物体的速度为v2 .
m1v0=m1v2+m2v1
v2=1m/s
小车与挡板碰后至小车与滑块再次相对静止的过程中,小车与滑块为系统动量守恒,设共速为v
m1v2-m2v1=(m1+m2)v
解得:v=0
因小车与挡板碰撞时无机械能损失,据能量转化与守恒有
μm1gL=
| 1 |
| 2 |
| v | 2 0 |
解得:L=1m
(3)若小车与挡板即将发生第n次碰撞之前,小车与物块的动量大小相等,则在小车与挡板第n次碰撞之后,据动量守恒可确定两者相对静止时,整体共同速度为零,系统末动能为零.这样的条件下物块相对小车静止在另外一端.
令小车运动的加速度,据牛顿第二定律有:μm1g=m2a1
解得:a1=
| 4 |
| 3 |
小车由静止开始匀加速至与挡板发生第一次碰撞之前,用时为t0
d=
| 1 |
| 2 |
| t | 2 0 |
此时小车的速度 v=a1t0
至小车即将与挡板发生第n次碰撞之前,用时t=(2n-1)t0
此时,物块速度为 v′,v′=v0-a2t
且 m1v=m2v′
代入数据联解可得:t0=
| 1 |
| 2n |
d=
| 1 |
| 6n2 |
答:(1)即将与挡板P相撞时小车的速度为
| 2 |
| 3 |
(2)小车长L为1m;
(3)能让小物块刚好在车面右端保持相对静止d的所有可能取值为 d=
| 1 |
| 6n2 |
点评:本题过程非常复杂,关键要把握每个过程的物理规律,对于系统,考虑动量守恒和能量守恒.第3小问,相当于数列问题,关键经总结出规律进行求解.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 (2009?天津)如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求
(2009?天津)如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求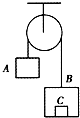 如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力,在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )
如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力,在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )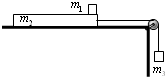 如图所示,质量m2=4kg、长L=1.5m的长木板置于光滑水平桌面上,再将m1=2kg的另一物块(可视为质点)置于长木板的最右端,物块与长木板间的动摩擦因数为μ=0.4,一根水平细绳通过定滑轮将另一物块m3与长木板相连,手持m3使细绳刚好伸直,设最大静摩擦力等于滑动摩擦力,开始时m2距滑轮足够远,桌面足够高.(g取10m/s2)
如图所示,质量m2=4kg、长L=1.5m的长木板置于光滑水平桌面上,再将m1=2kg的另一物块(可视为质点)置于长木板的最右端,物块与长木板间的动摩擦因数为μ=0.4,一根水平细绳通过定滑轮将另一物块m3与长木板相连,手持m3使细绳刚好伸直,设最大静摩擦力等于滑动摩擦力,开始时m2距滑轮足够远,桌面足够高.(g取10m/s2) (2011?河南模拟)如图所示,质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行,长木板保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与水平地面间的动摩擦因数为μ2,则( )
(2011?河南模拟)如图所示,质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行,长木板保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与水平地面间的动摩擦因数为μ2,则( )