题目内容
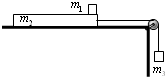 如图所示,质量m2=4kg、长L=1.5m的长木板置于光滑水平桌面上,再将m1=2kg的另一物块(可视为质点)置于长木板的最右端,物块与长木板间的动摩擦因数为μ=0.4,一根水平细绳通过定滑轮将另一物块m3与长木板相连,手持m3使细绳刚好伸直,设最大静摩擦力等于滑动摩擦力,开始时m2距滑轮足够远,桌面足够高.(g取10m/s2)
如图所示,质量m2=4kg、长L=1.5m的长木板置于光滑水平桌面上,再将m1=2kg的另一物块(可视为质点)置于长木板的最右端,物块与长木板间的动摩擦因数为μ=0.4,一根水平细绳通过定滑轮将另一物块m3与长木板相连,手持m3使细绳刚好伸直,设最大静摩擦力等于滑动摩擦力,开始时m2距滑轮足够远,桌面足够高.(g取10m/s2)(1)要使m3由静止释放后,物块m1与m2不发生相对运动,求m3的取值范围.
(2)去掉m3,用大小为40N的拉力向下拉细绳,作用0.5s后撤去拉力,求m1的最终速度.
分析:(1)要使m3由静止释放后,物块m1与m2恰好不发生相对运动时,两者之间的静摩擦力达到最大,对m1,由牛顿第二定律求出最大加速度,再对m1和m2整体及m3,由牛顿第二定律列式,即可求得m3的取值范围.
(2)去掉m3,用大小为40N的拉力向下拉细绳,根据上题的结果可知物块在木板上滑动.由牛顿第二定律和运动学公式求出0.5s时两个物体的速度和位移,得知物块在木板上继续滑动,当两者相对静止时,根据动量守恒求出相对静止时的共同速度,由能量守恒列式求出相对滑动的位移,即可得到m1的最终速度.
(2)去掉m3,用大小为40N的拉力向下拉细绳,根据上题的结果可知物块在木板上滑动.由牛顿第二定律和运动学公式求出0.5s时两个物体的速度和位移,得知物块在木板上继续滑动,当两者相对静止时,根据动量守恒求出相对静止时的共同速度,由能量守恒列式求出相对滑动的位移,即可得到m1的最终速度.
解答:解:(1)物块m1与m2不发生相对运动时,m1的最大加速度满足:μmg=ma,a=μg
对于m1和m2整体:T=(m1+m2)a
对于m3:m3g-T=m3a
代入数据得:m3=4kg
故m3的取值范围为m3≤4kg
(2)上题中绳子的拉力小于40N,所以去掉m3,用大小为40N的拉力向下拉细绳,物块将在木板上滑动.
设力F拉细绳时,m1、m2的加速度为a1、a2
对于m1,有 μm1g=m1a
s1=
a1t2 v1=a1t
对于m2,有 F-μm2g=m2a2
s2=
a2t2 v2=a2t
代入数据得 a1=4m/s2 a2=8m/s2 s1=0.5m s2=1m
v1=2m/s v2=4m/s
由于△s1=s2-s1=0.5m<1m,故物块在木板上继续滑动.
撤去F后,系统动量守恒,设物块能在木板上跟木板相对静止,则有:
m1v1+m2v2=(m1+m2)v
μm1g△s2=
m1
+
m2
-
(m1+m2)v2
代入数据得△s2=0.67m,v=3.33m/s
由于△s1+△s2=1.17m<1.5m,故物块最后的速度为3.33m/s.
答:(1)要使m3由静止释放后,物块m1与m2不发生相对运动,m3的取值范围m3≤4kg.
(2)去掉m3,用大小为40N的拉力向下拉细绳,作用0.5s后撤去拉力,m1的最终速度是3.33m/s.
对于m1和m2整体:T=(m1+m2)a
对于m3:m3g-T=m3a
代入数据得:m3=4kg
故m3的取值范围为m3≤4kg
(2)上题中绳子的拉力小于40N,所以去掉m3,用大小为40N的拉力向下拉细绳,物块将在木板上滑动.
设力F拉细绳时,m1、m2的加速度为a1、a2
对于m1,有 μm1g=m1a
s1=
| 1 |
| 2 |
对于m2,有 F-μm2g=m2a2
s2=
| 1 |
| 2 |
代入数据得 a1=4m/s2 a2=8m/s2 s1=0.5m s2=1m
v1=2m/s v2=4m/s
由于△s1=s2-s1=0.5m<1m,故物块在木板上继续滑动.
撤去F后,系统动量守恒,设物块能在木板上跟木板相对静止,则有:
m1v1+m2v2=(m1+m2)v
μm1g△s2=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
代入数据得△s2=0.67m,v=3.33m/s
由于△s1+△s2=1.17m<1.5m,故物块最后的速度为3.33m/s.
答:(1)要使m3由静止释放后,物块m1与m2不发生相对运动,m3的取值范围m3≤4kg.
(2)去掉m3,用大小为40N的拉力向下拉细绳,作用0.5s后撤去拉力,m1的最终速度是3.33m/s.
点评:本题是连接体问题,关键要理清物体的运动情况,抓住临界条件:物块m1与m2恰好不发生相对运动时,两者之间的静摩擦力达到最大;第2题中,撤去拉力后,根据两个物体相对静止时的共同速度和位移关系求解第2题,考查分析和解决物理综合题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009?天津)如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求
(2009?天津)如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求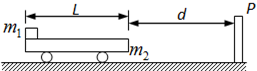 如图所示,质量m2=0.3kg的小车静止在光滑的水平面上,距车的右端
如图所示,质量m2=0.3kg的小车静止在光滑的水平面上,距车的右端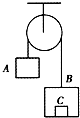 如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力,在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )
如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力,在箱子加速下落的过程中,取g=10m/s2,下列正确的是( ) (2011?河南模拟)如图所示,质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行,长木板保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与水平地面间的动摩擦因数为μ2,则( )
(2011?河南模拟)如图所示,质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行,长木板保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与水平地面间的动摩擦因数为μ2,则( )