题目内容
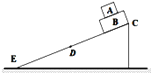
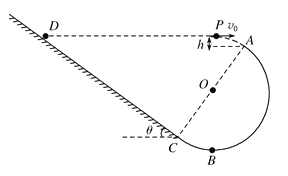
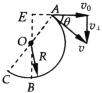
【题目】如图所示,半径为R的光滑半圆轨道ABC与倾角为θ=37°的粗糙斜面轨道DC相切于C,圆轨道的直径AC与斜面垂直.质量为m的小球从A点左上方距A高为h的斜面上方P点以某一速度水平抛出,刚好与半圆轨道的A点相切进入半圆轨道内侧,之后经半圆轨道沿斜面刚好滑到与抛出点等高的D处.已知当地的重力加速度为g,取R=![]() h,sin37°=0.6,cos37°=0.8,不计空气阻力,求:
h,sin37°=0.6,cos37°=0.8,不计空气阻力,求:
(1)小球被抛出时的速度v0;
(2)小球到达半圆轨道最低点B时,对轨道的压力大小;
(3)小球从C到D过程中摩擦力做的功W.
【答案】(1)小球被抛出时的速度v0是![]() .
.
(2)小球到达半圆轨道最低点B时,对轨道的压力大小是5.6mg,方向竖直向下.
(3)小球从C到D过程中摩擦力做的功W是﹣![]() .
.
【解析】解:(1)小球到达A点时,速度与水平方向的夹角为θ,如图所示.
则有①
由几何关系得 v0=v1cotθ②
得③
(2)A、B间竖直高度H=R(1+cosθ)④
设小球到达B点时的速度为v,则从抛出点到B过程中,根据机械能守恒有
![]() ⑤
⑤
在B点,有![]() ⑥
⑥
联立解得 FN=5.6mg⑦
由牛顿第三定律知,小球在B点对轨道的压力大小是FN′=FN=5.6mg,方向竖直向下⑧
(3)整个运动知过程中,重力做功为零,根据动能定理得知:小球沿斜面上滑过程中克服摩擦力做的功等于小球做平抛运动的初动能,有W=0﹣![]() =﹣
=﹣![]() ⑨
⑨
答:(1)小球被抛出时的速度v0是![]() .
.
(2)小球到达半圆轨道最低点B时,对轨道的压力大小是5.6mg,方向竖直向下.
(3)小球从C到D过程中摩擦力做的功W是﹣![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目