Question

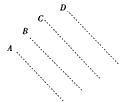
【题目】如图所示，在竖直平面内有一质量m＝0.5 kg、电荷量q＝＋2×10－3 C的带电小球，有一根长L＝0.1 m且不可伸长的绝缘轻细线系在一方向水平向右、分布的区域足够大的匀强电场中的O点.已知A、O、C点等高，且OA＝OC＝L，若将带电小球从A点无初速度释放，小球到达最低点B时速度恰好为零，g取10 m/s2.

(1)求匀强电场的电场强度E的大小；

(2)求小球从A点由静止释放运动到B点的过程中速度最大时细线的拉力大小；

(3)若将带电小球从C点无初速度释放，求小球到达B点时细线张力大小.

Answer 1

【答案】（1）2.5×103 N/C（2）(15－10) N（3）15N

【解析】

(1)小球到达最低点B时速度为零，则

0＝mgL－EqL.

E＝2.5×103 N/C

(2) 小球到达最低点B时速度为零，根据对称性可知，达到最大速度的位置为AB弧的中点，即当沿轨迹上某一点切线方向的合力为零时，小球的速度有最大值，由动能定理有

mv2－0＝mgLsin 45°－Eq(L－Lcos 45°).

m＝F－2mgcos 45°.

F＝(15－10) N.

(3)小球从C运动到B点过程，由动能定理得

.

解得：

在B点

以上各式联立解得

T=15N.