题目内容
(10分)已知地球半径为R,地球表面的重力加速度为g,地球同步卫星的周期为To。另有一颗
轨道在赤道平面内的绕地球自西向东运行的卫星,某时刻该卫星能观察到的赤道弧长最大为 赤道周长的三分之一。求:
(1)该卫星的周期。 ,
(2)该卫星相邻两次经过地球赤道上同一点的正上空所需的时间。
(1)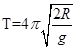 (2)
(2)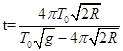
解析试题分析:(1)因在该卫星上能观察到的地球赤道弧长为赤道周长的三分之一,则可知该圆弧对应的圆心角为120°,结合几何关系知:
该卫星的轨道半径 (2分)
(2分)
设该卫星的质量为m,周期为T,地球的质量为M,则有: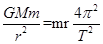 r (2分)
r (2分)
由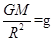 有:
有: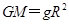 (1分)
(1分)
解得: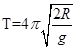 。 (1分)
。 (1分)
(2)设该卫星相邻两次经过地球赤道上同一点的正上空所需的时间为t,有: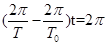 (2分)
(2分)
解得: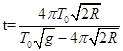 。 (2分)
。 (2分)
考点:万有引力与航天

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
全球定位系统(GPS)有24颗卫星分布在绕地球的6个轨道上运行,距地面的高度都为2万千米.已知地球同步卫星离地面的高度为3.6万千米,地球半径约为6 400 km,则全球定位系统的这些卫星的运行速度约为( )
| A.3.1 km/s | B.3.9 km/s |
| C.7.9 km/s | D.11.2 km/s |
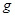 ,地球的自转周期为
,地球的自转周期为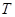 ,卫星在同步圆轨道上的轨道半径为
,卫星在同步圆轨道上的轨道半径为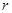 ,求:地球的半径?
,求:地球的半径?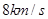 )
)