Question

【题目】在如图所示，在竖直面内的直角坐标系中，x坐标轴在水平地面上，A、B、C三个小球沿图示方向做平抛运动，下列表述正确的是

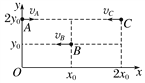
A. 若A、B、C同时抛出，只需满足vC>vB>vA，就恰好能同时在地面相遇

B. 若A、B能在地面相遇，则A、B在空中运动的时间之比为2∶1

C. 若A、C在(x0，0)相遇，则一定满足vA＝vC

D. 若B、C同时开始做平抛运动，二者绝不可能在空中相遇

Answer 1

【答案】CD

【解析】若A、B、C处三球同时抛出，但是A、C两球的竖直高度与B不同，竖直分运动均是自由落体运动，故A处、C处球不可能与B处球相遇，故A错误；若A、B处两球能在地面相遇，根据h=gt2可知，两个球运动时间之比为：1，故B错误；若A、C处两球在(x0，0)点相遇，由于水平分运动是匀速直线运动，水平分位移相等，时间也相等，故水平分速度相等，即初速度相等，一定满足vA＝vC，故C正确；由于平抛运动的竖直分运动是自由落体运动，故只要B、C处两球同时开始做平抛运动，二者不可能在空中相遇，故D正确；故选CD.