题目内容
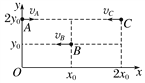
【题目】某同学讲小球从P点水平抛向固定在水平地面上的圆柱形桶,小球沿着桶的直径方向恰好从桶的左侧上边沿进入桶内并打在桶的底角,如图所示,已知P点到桶左边沿的水平距离s=0.80m,桶的高度![]() ,直径d=0.20m,桶底和桶壁的厚度不计,取重力加速度
,直径d=0.20m,桶底和桶壁的厚度不计,取重力加速度![]() ,求:
,求:
(1)P点离地面的高度![]() 和小球抛出时的速度大小
和小球抛出时的速度大小![]() ;
;
(2)小球经过桶的左侧上边沿时的速度大小及速度方向与水平方向的夹角正切值(结果可以带根号)。

【答案】(1)1.25m, ![]() ;(2)
;(2)![]() ,2.
,2.
【解析】试题分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合运动学公式即可求出P点离地面的高度和小球抛出时的速度大小;把速度进行分解,求出竖直速度,在进行合成即可求出球经过桶的左侧上边沿时的速度大小及速度方向与水平方向的夹角正切值。
(1)设小球从P点运动到圆桶左上沿的时间为t1、运动到桶的底角的总时间为t2,
由平抛运动的规律有:从P点运动到圆桶上沿过程中在竖直方向有: ![]()
在水平方向有:s=v0t1
从P点运动到桶的底角过程中在竖直方向有: ![]()
在水平方向有:s+d=v0t2
联立以上并代入数据可得:h1=1.25m v0=2.0m/s
(2)设小球运动到桶的左侧上沿时速度大小为v1,与水平方向的夹角为θ
由平抛运动的规律有:竖直方向的速度:v⊥=gt1
此时小球的速度: ![]() ,
,
代入数据解得: ![]()
速度的方向为: ![]()
代入数据解得:tanθ=2

练习册系列答案
相关题目