��Ŀ����
����Ŀ����ͼ��ʾ����һ���![]() �����
�����![]() ���㹻��ƽ�н�������
���㹻��ƽ�н�������![]() ��
��![]() �˽�����ֵ
�˽�����ֵ![]() �ĵ��裬����
�ĵ��裬����![]() �Ľ�����
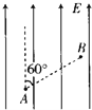
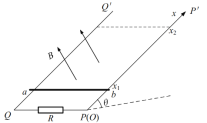
�Ľ�����![]() ��ֱ������ã�����ԭ��λ�ڵˡ������ص������ϵ�������x���ڵ���������д�ֱ����ƽ�����ϵĴų����ų���С��x�᷽��仯����
��ֱ������ã�����ԭ��λ�ڵˡ������ص������ϵ�������x���ڵ���������д�ֱ����ƽ�����ϵĴų����ų���С��x�᷽��仯����![]() ��ϵ����
��ϵ����![]() ʱ���𣬰�
ʱ���𣬰�![]() ������F�����£���
������F�����£���![]() ��б�������˶���
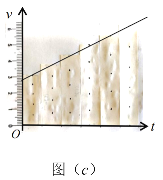
��б�������˶���![]() �������ٶ�v��λ��x�Ĺ�ϵ����
�������ٶ�v��λ��x�Ĺ�ϵ����![]() ����
����![]() ʼ�ձ����뵼�촹ֱ�������������裬��������Ħ�����������ٶ�gȡ
ʼ�ձ����뵼�촹ֱ�������������裬��������Ħ�����������ٶ�gȡ![]() ������ʾ������
������ʾ������![]() ͼ���µ����������������F���Ĺ�����
ͼ���µ����������������F���Ĺ�����
��1����![]() �˶���
�˶���![]() ��ʱ�����˵��Ʋ�
��ʱ�����˵��Ʋ�![]() ������R���ĵĵ繦��P��
������R���ĵĵ繦��P��
��2������F�ڴ��˶������������Ĺ���
��3������F�ڴ��˶������е�ƽ�����ʣ�
���𰸡���1�� 0.1V 0.1W ��2����0.976J ��3����4.07W
��������
(1)��ab�˶���x2��ʱ�����˵��Ʋ
Uab��B1lv1��2x1l![]() ��0.1V
��0.1V
���ݵ繦�ʵļ��㹫ʽ�ɵã�
![]()
(2)���ݶ��ܶ����ɵã�WF��WG��WA��![]()
����
WG��mgsin����x2��x1����0.2J
��������
![]()
������������
![]()
�����ɵã�
WF����0.976J
(3)���ݱպϵ�·ŷķ���ɿɵû�·�ĵ�����
![]()
��Ϊ�����㶨����I2R��t��WA
��ã�
��t��0.24s
ƽ������Ϊ��
![]()

 ��������ϵ�д�
��������ϵ�д�����Ŀ����ͼ��ʾ��һ����Ϊ1kg�����徲ֹ���ڴֲڳ̶���ͬ��ˮƽ���ϡ���![]() ʱ�̣�������ʩ��һ��ˮƽ�����
ʱ�̣�������ʩ��һ��ˮƽ�����![]() �ǵ���
�ǵ���![]() �����ã��������ȼ���ֱ���˶�һ��ʱ���ȥ��
�����ã��������ȼ���ֱ���˶�һ��ʱ���ȥ��![]() ������ͣ��ˮƽ���ϡ���
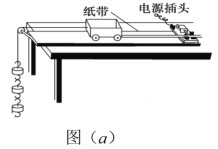
������ͣ��ˮƽ���ϡ���![]() ʱ�̿�ʼ��ÿ��0.1sͨ���ٶȴ����������������˲ʱ�ٶȣ������˶������еIJ��ֲ����������±���ʾ����֪
ʱ�̿�ʼ��ÿ��0.1sͨ���ٶȴ����������������˲ʱ�ٶȣ������˶������еIJ��ֲ����������±���ʾ����֪![]() ��
��![]() ����
����
| �� | 0.3 | �� | 1.6 | 1.7 | 1.8 | �� |
| �� | 1.8 | �� | 3.0 | 2.5 | 2.0 | �� |
(1)��![]() �Ĵ�С��
�Ĵ�С��
(2)�����˶������л�õ�����ܣ�
(3)�����˶�����������˷�Ħ���������Ĺ���