题目内容
4. 如图所示,一个质量均匀分布的半径为R的球体对球外质点P的万有引力为F.如果在球体中央挖去半径为r的一部分球体,且r=$\frac{R}{2}$,则原球体剩余部分对质点P的万有引力变为( )
如图所示,一个质量均匀分布的半径为R的球体对球外质点P的万有引力为F.如果在球体中央挖去半径为r的一部分球体,且r=$\frac{R}{2}$,则原球体剩余部分对质点P的万有引力变为( )| A. | $\frac{1}{2}$F | B. | $\frac{1}{8}$F | C. | $\frac{7}{8}$F | D. | $\frac{1}{4}$F |
分析 用没挖之前球对小球的引力,减去被挖部分对小球的引力,就是剩余部分对质点的引力.结合万有引力定律公式进行求解.
解答 解:根据m=$ρ\frac{4}{3}π{r}^{3}$知,挖去部分的小球是整个实心球质量的$\frac{1}{8}$,
挖去部分的质量m=$\frac{1}{8}M$,
设没挖去前,对小球的引力F=$G\frac{M{m}_{0}}{{R}^{2}}$,
挖去的部分对质点的引力$F′=\frac{Gm{m}_{0}}{{R}^{2}}$=$\frac{1}{8}F$,
则剩余部分对质点P的引力$F″=F-F′=\frac{7}{8}F$.
故选:C.
点评 本题的关键就是要对挖之前的引力和挖去部分的引力计算,因为挖去后重心还在圆心,也可以通过万有引力定律公式直接求解,注意若不在圆心处挖去,不能运用公式直接去计算剩余部分的引力,因为那是一个不规则球体.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
14. 如图所示的分压器电路,A、B为分压器的输出端,若把滑动变阻器的滑动片P置于变阻器中央,下列判断正确的是( )
如图所示的分压器电路,A、B为分压器的输出端,若把滑动变阻器的滑动片P置于变阻器中央,下列判断正确的是( )
 如图所示的分压器电路,A、B为分压器的输出端,若把滑动变阻器的滑动片P置于变阻器中央,下列判断正确的是( )
如图所示的分压器电路,A、B为分压器的输出端,若把滑动变阻器的滑动片P置于变阻器中央,下列判断正确的是( )| A. | 空载时输出电压UAB=$\frac{{U}_{CD}}{2}$ | |
| B. | 当接上负载R时,输出电压UAB<$\frac{{U}_{CD}}{2}$ | |
| C. | 负载R越大,UAB越接近$\frac{{U}_{CD}}{2}$ | |
| D. | 负载R越小,UAB越接近$\frac{{U}_{CD}}{2}$ |
12.在地球表面不同纬度的物体,因随地球自转而做匀速圆周运动,下列说法中正确的是( )
| A. | 这些物体运动的角速度相同 | B. | 这些物体运动的线速度相同 | ||
| C. | 这些物体运动向心加速度相同 | D. | 这些物体运动的线速度大小相等 |
19.由于受太阳系中辐射出的高能射线和卫星轨道所处的空间存在极其稀薄的大气影响,对我国神州飞船与天宫目标飞行器在离地面343km的近圆形轨道上的载人空间交会对接.下面说法正确的是( )
| A. | 为实现对接,两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间 | |
| B. | 如不加干预,在运行一段时间后,天宫一号的动能可能会减小 | |
| C. | 如不加干预,天宫一号的轨道高度将缓慢降低 | |
| D. | 航天员在天宫一号中处于失重状态,说明航天员不受地球引力作用 |
16.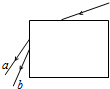 如图所示,一束复色光从长方体玻璃砖上表面射入玻璃,穿过玻璃砖后从侧表面射出,变为a、b两束单色光,这两束单色光相比较下列说法正确的是( )
如图所示,一束复色光从长方体玻璃砖上表面射入玻璃,穿过玻璃砖后从侧表面射出,变为a、b两束单色光,这两束单色光相比较下列说法正确的是( )
 如图所示,一束复色光从长方体玻璃砖上表面射入玻璃,穿过玻璃砖后从侧表面射出,变为a、b两束单色光,这两束单色光相比较下列说法正确的是( )
如图所示,一束复色光从长方体玻璃砖上表面射入玻璃,穿过玻璃砖后从侧表面射出,变为a、b两束单色光,这两束单色光相比较下列说法正确的是( )| A. | 在玻璃中b光的全反射临界角较小 | B. | 玻璃对a光的折射率较大 | ||
| C. | 在真空中a光波长较短 | D. | 在玻璃中b光传播速度较大 |
14.对于一块普通指针钟表,则( )
| A. | 分针的转动周期为1小时 | |
| B. | 时针的转动周期为24小时 | |
| C. | 若分针的长度是时针的2倍,分针端点的线速度分针是时针的24倍 | |
| D. | 若分针的长度是时针的2倍,分针端点的线速度分针是时针的48倍 |
 某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:
某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想: 如图所示,相距为L的两条足够长的光滑平行金属导轨固定在水平面上,导轨由两种材料组成.PG右侧部分单位长度电阻为r0,且PQ=QH=GH=L.PG左侧导轨电阻不计,导体棒AC的电阻为R0,整个导轨处于匀强磁场中,磁场方向垂直于导轨平面向下,磁感应强度大小为B.质量为m的导体棒AC在恒力F作用下从静止开始运动,在到达PG之前导体棒AC已经匀速.
如图所示,相距为L的两条足够长的光滑平行金属导轨固定在水平面上,导轨由两种材料组成.PG右侧部分单位长度电阻为r0,且PQ=QH=GH=L.PG左侧导轨电阻不计,导体棒AC的电阻为R0,整个导轨处于匀强磁场中,磁场方向垂直于导轨平面向下,磁感应强度大小为B.质量为m的导体棒AC在恒力F作用下从静止开始运动,在到达PG之前导体棒AC已经匀速. 如图,一长木板位于光滑水平面上,长木板的左端固定一挡板,木板和挡板的总质量为M=3.0kg,木板的长度为L=1.5m.在木板右端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速度v0沿木板向左滑动,重力加速度g取10m/s2.
如图,一长木板位于光滑水平面上,长木板的左端固定一挡板,木板和挡板的总质量为M=3.0kg,木板的长度为L=1.5m.在木板右端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速度v0沿木板向左滑动,重力加速度g取10m/s2.