题目内容
14. 在光滑水平面上放有一个质量为M斜劈,它的斜面也是光滑的,在斜面上放一个质量为m的物体.现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,如图,已知斜劈倾角为θ,则斜劈对物体m的弹力大小为( )
在光滑水平面上放有一个质量为M斜劈,它的斜面也是光滑的,在斜面上放一个质量为m的物体.现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,如图,已知斜劈倾角为θ,则斜劈对物体m的弹力大小为( )| A. | mgcosθ | B. | $\frac{mg}{cosθ}$ | C. | $\frac{mF}{{({M+m})sinθ}}$ | D. | m$\sqrt{{g^2}+{{({\frac{F}{M+m}})}^2}}$ |
分析 对物块受力分析,其受到两个力的作用:重力,斜面支持力.由受力分解和牛顿第二定律及勾股定理可以得到斜面对m的弹力的表达式.
解答 解:对物块受力分析: 其合力沿水平向左,故:
其合力沿水平向左,故:
$N=\frac{mg}{cosθ}$
由对整体受力,其水平受力为:向左的推力F,用牛顿第二定律得:
F=(M+m)a
解得:$a=\frac{F}{M+m}$
对m来说,其合力为:F′=Nsinθ
由牛顿第二定律:
F′=ma
Nsinθ=m$\frac{F}{M+m}$
解得:$\frac{mF}{(M+m)sinθ}$
根据勾股定理可知,
N2=(mg)2+(ma)2=m$\sqrt{{g}^{2}+{(\frac{F}{M+m})}^{2}}$,故BCD正确,A错误;
故选:BCD
点评 本题考查牛顿第二定律的应用;要明确物体的受力和运动状态,是解答本题的关键,也是出现两个表达式的原因.

练习册系列答案
相关题目
5.关于电动势E,下列说法正确的是( )
| A. | 电动势E的大小,与非静电力做的功W的大小成正比,与移送电荷量q的大小成反比 | |
| B. | 电动势E是由电源本身决定的,跟电源的体积和外电路均无关 | |
| C. | 电动势E的单位与电势、电势差的单位都是伏特 | |
| D. | 电动势E是表征电源把其他形式的能转化为电能本领的物理量 |
2.如图所示,匀强磁场中放着通入相同电流的几段导线(均在纸面内),A、B端间距离都相等,受力的情况是( )
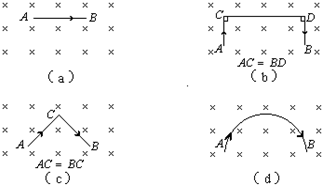

| A. | 图(a)受力最小 | B. | 各图受力方向相同 | ||
| C. | 各图受力一样 | D. | 不能确定 |
3.某质点的位移随时间的变化关系为x=4t-2t2,单位均为国际单位制单位,那么它的初速度和加速度分别是( )
| A. | 4m/s,-4m/s2 | B. | 4m/s,4m/s2? | C. | 4m/s,2m/s2 | D. | 4m/s,-2m/s2 |





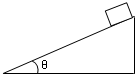 一个体积可以不计的物体,从倾角为θ的斜面顶端由静止开始匀加速下滑,若斜面长L,物体与斜面间的摩擦因数为μ.求:
一个体积可以不计的物体,从倾角为θ的斜面顶端由静止开始匀加速下滑,若斜面长L,物体与斜面间的摩擦因数为μ.求: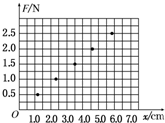 一位同学做“探究形变与弹力的关系”的实验.这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据在图中坐标上已描出:
一位同学做“探究形变与弹力的关系”的实验.这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据在图中坐标上已描出: