题目内容
4．
一位同学做“探究形变与弹力的关系”的实验．这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据在图中坐标上已描出：①在图中的坐标上作出F-x图线．
②写出曲线的函数表达式（x用cm作单位）：F=0.44x．
分析 以纵轴表示弹簧的弹力，横轴表示弹簧的伸长量，描点作图．让尽量多的点落在直线上或分居直线两侧．根据F与x成正比关系，写出表达式．表达式中的常数表示弹簧的劲度系数
解答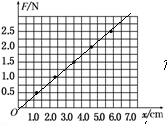 
解：①用描点法作图．如下图．
②图象的斜率k=$\frac{2.0}{4.5}$N/cm=0.44N/cm
根据图象，该直线为过原点的一条直线，即弹力与伸长量成正比，即F=kx=0.44x（N）．式中的常数表示弹簧的劲度系数．
故答案为：（1）如图；（2）F=0.44x（N）．
点评 解决本题的关键掌握弹力与弹簧伸长关系的实验步骤，会描点作图，掌握作图的方法．会从图象中分析数据．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
14．
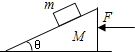在光滑水平面上放有一个质量为M斜劈，它的斜面也是光滑的，在斜面上放一个质量为m的物体．现用一水平力F推斜劈，恰使物体m与斜劈间无相对滑动，如图，已知斜劈倾角为θ，则斜劈对物体m的弹力大小为（ ）
在光滑水平面上放有一个质量为M斜劈，它的斜面也是光滑的，在斜面上放一个质量为m的物体．现用一水平力F推斜劈，恰使物体m与斜劈间无相对滑动，如图，已知斜劈倾角为θ，则斜劈对物体m的弹力大小为（ ）| A． | mgcosθ | B． | $\frac{mg}{cosθ}$ | C． | $\frac{mF}{{（{M+m}）sinθ}}$ | D． | m$\sqrt{{g^2}+{{（{\frac{F}{M+m}}）}^2}}$ |
19．
如图所示，虚线所示的区域内有方向垂直纸面的匀强磁场，一束速度大小各不相同的质子正对该区域的圆心O射入这个磁场．发现有的质子在磁场里运动的时间长，有的较短，其中运动时间较长的质子（ ）
如图所示，虚线所示的区域内有方向垂直纸面的匀强磁场，一束速度大小各不相同的质子正对该区域的圆心O射入这个磁场．发现有的质子在磁场里运动的时间长，有的较短，其中运动时间较长的质子（ ）| A． | 入射的速度一定较大 | B． | 在该磁场中运动路程一定较长 | ||
| C． | 在该磁场中偏转的角度一定较大 | D． | 出射的速度一定较小 |
9．
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系，进行了如下实验：在离地面高度为h的光滑水平桌面上，沿着与桌子边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的一个小钢球接触．当弹簧处于自然长度时，小钢球恰好在桌子边缘，如图所示．让钢球向左压缩弹簧一段距离后由静止释放，使钢球沿水平方向射出桌面，小钢球在空中飞行后落在水平地面上，水平距离为s．
（1）小刚球离开桌面时的速度大小为v=s$\sqrt{\frac{g}{2h}}$，，弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=$\frac{m{gs}^{2}}{4h}$．
（2）弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如表所示：
由实验数据，可确定弹性势能Ep与弹簧的压缩量x的关系为C（式中k为比例系数）
（A）Ep=kx （B）Ep=k$\sqrt{x}$ （C）Ep=kx2 （D）Ep=k$\frac{1}{x}$．
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系，进行了如下实验：在离地面高度为h的光滑水平桌面上，沿着与桌子边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的一个小钢球接触．当弹簧处于自然长度时，小钢球恰好在桌子边缘，如图所示．让钢球向左压缩弹簧一段距离后由静止释放，使钢球沿水平方向射出桌面，小钢球在空中飞行后落在水平地面上，水平距离为s．（1）小刚球离开桌面时的速度大小为v=s$\sqrt{\frac{g}{2h}}$，，弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=$\frac{m{gs}^{2}}{4h}$．
（2）弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如表所示：
| 弹簧的压缩量x （cm） | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小钢球飞行的水平距离s （m） | 2.01 | 3.00 | 4.01 | 4.96 | 6.01 | 7.00 |
（A）Ep=kx （B）Ep=k$\sqrt{x}$ （C）Ep=kx2 （D）Ep=k$\frac{1}{x}$．
在“用油膜法估测分子大小”实验中所用的油酸酒精溶液的浓度为1 000mL溶液中有纯油酸0.6mL，用注射器测得1mL上述溶液为80滴，把1滴该溶液滴入盛水的浅盘内，让油膜在水面上尽可能散开，测得油酸薄膜的轮廓形状和尺寸如图所示，图中正方形方格的边长为1cm．
13．如图所示，是用悬线悬挂的电灯，下列说法中正确的是（ ）
| A． | 电灯对悬线的拉力与电灯所受的重力是平衡力 | |
| B． | 电灯对悬线的拉力与线对顶的拉力是平衡力 | |
| C． | 悬线对电灯的拉力与顶对悬线的拉力是作用力和反作用力 | |
| D． | 悬线对电灯的拉力与电灯对悬线的拉力是作用力和反作用力 |
14．短跑运动员在100m的比赛中，测得他在5s末的速度是8.7m/s，10s末到达终点时的速度为10.3m/s，此运动员在这100m中有关说法正确的是（ ）
| A． | 运动员在这100m中的平均速度是（8.7m/s+10.3m/s）/2=9.5m/s | |
| B． | 运动员在这100m中的平均速度是10m/s | |
| C． | 10.3m/s为瞬时速度 | |
| D． | 不能求出前5秒平均速度 |