题目内容
19.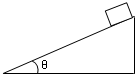 一个体积可以不计的物体,从倾角为θ的斜面顶端由静止开始匀加速下滑,若斜面长L,物体与斜面间的摩擦因数为μ.求:
一个体积可以不计的物体,从倾角为θ的斜面顶端由静止开始匀加速下滑,若斜面长L,物体与斜面间的摩擦因数为μ.求:(1)物体下滑加速度的大小
(2)物体到达斜面中点的速度大小.
分析 根据牛顿第二定律求出物体下滑的加速度,结合速度位移公式求出物体到达底端时的速度.
解答 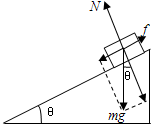 解:(1)如图,由牛顿第二定律有:
解:(1)如图,由牛顿第二定律有:
mgsinθ-f=ma…①
f=μN…②
N=mgcosθ…③
由①②③得:a=gsinθ-μgcosθ
(2)由v2=2a$\frac{L}{2}$
得:v=$\sqrt{gL({sinθ-μcosθ})}$
答:(1)物体下滑的加速度为gsinθ-μgcosθ.
(2)物体到达斜面底端时的速度为$\sqrt{gL({sinθ-μcosθ})}$.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,比较简单,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
9. 如图,已知L的电阻为20Ω,R是阻值0~80Ω的滑动变阻器,电源电压6V保持不变.在滑片滑动过程中,电压表、电流表示数的变化范围是( )
如图,已知L的电阻为20Ω,R是阻值0~80Ω的滑动变阻器,电源电压6V保持不变.在滑片滑动过程中,电压表、电流表示数的变化范围是( )
 如图,已知L的电阻为20Ω,R是阻值0~80Ω的滑动变阻器,电源电压6V保持不变.在滑片滑动过程中,电压表、电流表示数的变化范围是( )
如图,已知L的电阻为20Ω,R是阻值0~80Ω的滑动变阻器,电源电压6V保持不变.在滑片滑动过程中,电压表、电流表示数的变化范围是( )| A. | 0~1.2V 0.06~0.3A | B. | 6~1.2V 0.30~0.06 A | ||
| C. | 0~4.8V 0.3~0.06A | D. | 6~4.8V 0.06~0.3A |
14.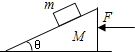 在光滑水平面上放有一个质量为M斜劈,它的斜面也是光滑的,在斜面上放一个质量为m的物体.现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,如图,已知斜劈倾角为θ,则斜劈对物体m的弹力大小为( )
在光滑水平面上放有一个质量为M斜劈,它的斜面也是光滑的,在斜面上放一个质量为m的物体.现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,如图,已知斜劈倾角为θ,则斜劈对物体m的弹力大小为( )
 在光滑水平面上放有一个质量为M斜劈,它的斜面也是光滑的,在斜面上放一个质量为m的物体.现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,如图,已知斜劈倾角为θ,则斜劈对物体m的弹力大小为( )
在光滑水平面上放有一个质量为M斜劈,它的斜面也是光滑的,在斜面上放一个质量为m的物体.现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,如图,已知斜劈倾角为θ,则斜劈对物体m的弹力大小为( )| A. | mgcosθ | B. | $\frac{mg}{cosθ}$ | C. | $\frac{mF}{{({M+m})sinθ}}$ | D. | m$\sqrt{{g^2}+{{({\frac{F}{M+m}})}^2}}$ |
4.以下说法正确的是( )
| A. | 加速度、路程、速度都是矢量 | B. | 位移、质量、速度、加速度都是矢量 | ||
| C. | 路程和质量都是标量 | D. | 位移、速度、加速度都是矢量 |
11.关于地球、太阳和月球的运动,下列说法正确的是( )
| A. | 以地球为参照系,月球是静止不动的 | |
| B. | 以地球为参照系,太阳在绕地球运动 | |
| C. | 以太阳为参照系,月球是在做圆周运动 | |
| D. | 以太阳为参照系,地球在绕太阳运动 |
9. 一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,进行了如下实验:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一个小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小钢球在空中飞行后落在水平地面上,水平距离为s.
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,进行了如下实验:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一个小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小钢球在空中飞行后落在水平地面上,水平距离为s.
(1)小刚球离开桌面时的速度大小为v=s$\sqrt{\frac{g}{2h}}$,,弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=$\frac{m{gs}^{2}}{4h}$.
(2)弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如表所示:
由实验数据,可确定弹性势能Ep与弹簧的压缩量x的关系为C(式中k为比例系数)
(A)Ep=kx (B)Ep=k$\sqrt{x}$ (C)Ep=kx2 (D)Ep=k$\frac{1}{x}$.
 一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,进行了如下实验:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一个小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小钢球在空中飞行后落在水平地面上,水平距离为s.
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,进行了如下实验:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一个小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小钢球在空中飞行后落在水平地面上,水平距离为s.(1)小刚球离开桌面时的速度大小为v=s$\sqrt{\frac{g}{2h}}$,,弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=$\frac{m{gs}^{2}}{4h}$.
(2)弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如表所示:
| 弹簧的压缩量x (cm) | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小钢球飞行的水平距离s (m) | 2.01 | 3.00 | 4.01 | 4.96 | 6.01 | 7.00 |
(A)Ep=kx (B)Ep=k$\sqrt{x}$ (C)Ep=kx2 (D)Ep=k$\frac{1}{x}$.
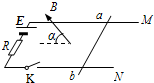 如图所示,水平放置的光滑金属导轨M、N平行地置于匀强磁场中,间距为d,磁场的磁感强度大小为B,方向与导轨平面夹角为α,金属棒ab的质量为m,放在导轨上且与导轨垂直.电源电动势为E,定值电阻的阻值为R,其余部分电阻不计.求开关闭合后:
如图所示,水平放置的光滑金属导轨M、N平行地置于匀强磁场中,间距为d,磁场的磁感强度大小为B,方向与导轨平面夹角为α,金属棒ab的质量为m,放在导轨上且与导轨垂直.电源电动势为E,定值电阻的阻值为R,其余部分电阻不计.求开关闭合后: