��Ŀ����
12�� ��ͼ��ʾ��һ�����㹻����ƽ�а������ˮƽ���ã���һ���ٶ�v0ˮƽ��������Ϊm�Ĵ����͵���ˮƽ���ҵij��ٶ�v0��������룬��ǡ������ͼ����ʾˮƽ����ͨ������������֪��������Ϊd����������һֱ����Դ������������ѹΪU���ֽ��¼�������$\frac{d}{3}$������˵����ȷ���ǣ�������
��ͼ��ʾ��һ�����㹻����ƽ�а������ˮƽ���ã���һ���ٶ�v0ˮƽ��������Ϊm�Ĵ����͵���ˮƽ���ҵij��ٶ�v0��������룬��ǡ������ͼ����ʾˮƽ����ͨ������������֪��������Ϊd����������һֱ����Դ������������ѹΪU���ֽ��¼�������$\frac{d}{3}$������˵����ȷ���ǣ�������| A�� | �����͵ν�����ƫת | |
| B�� | �����͵ν�������ˮƽ�����˶� | |
| C�� | �����͵������˶�������ʱ�Ķ��ܴ�СΪ$\frac{1}{4}$mgd+$\frac{1}{2}$mv02 | |
| D�� | �����͵������˶�������ʱ�Ķ��ܴ�СΪ$\frac{5}{12}$mgd+$\frac{1}{2}$mv02 |
���� ����ƽ���ϵ����ȷ������������������ٶԼ������ƺ���з����������˶��ĺϳɺͷֽ���ȷ����ˮƽ�����ϵ��˶������
����ƽ����������õ糡��������֮��Ĺ�ϵ���ٶ�ƽ���˶����ݶ��ܶ��������Һ�ε��ٶȺͶ��ܣ�
��� �⣺A���������⣬��ʼʱҺ�δӷ����������һֱ�������˶���˵���ܵ��������͵糡����С��ȣ������෴�����¼������ƣ�d��С��E���糡������Һ������ƫת���ڵ糡������ƽ���˶�������ˮƽ������ȻΪ�����˶�����A����B����
C����Һ�ε�ˮƽ�����˶�����ֱ�����������˶���
����������ѹΪU������Һ���ڰ���������˶�ʱ�У�mg-qE=0����
$E=\frac{U}{d}$����
���¼������ƺ�Һ���ڵ糡������ƽ���˶�ʱ�����ݶ��ܶ����У�$E��=\frac{U}{d-\frac{d}{3}}=\frac{3U}{2d}=\frac{3}{2}E$����
$��qE'-mg��\frac{d}{2}=\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2$����
������ô����͵������˶�������ʱ�Ķ��ܴ�С��${E}_{k}=\frac{1}{2}m{v}^{2}$=mgd+$\frac{1}{2}$mv02����C��ȷ��D����
��ѡ��C
���� ���⿼����������ڵ糡�е��˶������Ҫע����ȷ������������ȷ�˶����̣�����ƫת����Ҫע��Ӧ���˶��ĺϳɺͷֽ���з�����⣮

 ��ͼΪһ��г�Შ��t=0.10sʱ�̵IJ���ͼ��P��ƽ��λ��Ϊx=1m�����ʵ㣬�˿�P��������y������������0.2s�����һ��ȫ��Q��ƽ��λ��Ϊx=4m�����ʵ㣬������
��ͼΪһ��г�Შ��t=0.10sʱ�̵IJ���ͼ��P��ƽ��λ��Ϊx=1m�����ʵ㣬�˿�P��������y������������0.2s�����һ��ȫ��Q��ƽ��λ��Ϊx=4m�����ʵ㣬������| A�� | ����x�Ḻ���� | |
| B�� | t=0.05 sʱ���ʵ�Q�ļ��ٶ�Ϊ0���ٶ�Ϊ������� | |
| C�� | ��t=0.10 s��t=0.15 s���ò���x�ᴫ���ľ�����2 m | |
| D�� | ��t=0.10 s��t=0.15 s���ʵ�Pͨ����·��Ϊ10 cm | |
| E�� | t=0.25 sʱ���ʵ�Q������Ϊ10 cm |
 �õ糡���ܺ�ֱ�ۡ��ܷ���رȽϵ糡�и���ij�ǿ��С�뷽����ͼ���������������ֵ����γɵ糡�ĵ糡�ߣ�A��B�ǵ糡�е����㣬������
�õ糡���ܺ�ֱ�ۡ��ܷ���رȽϵ糡�и���ij�ǿ��С�뷽����ͼ���������������ֵ����γɵ糡�ĵ糡�ߣ�A��B�ǵ糡�е����㣬������| A�� | EA��EB������ͬ | B�� | EA��EB��������ͬ | C�� | EA��EB������ͬ | D�� | EA��EB��������ͬ |
| A�� | �糡ǿ��Ϊ��ĵط�������ҲΪ�� | |
| B�� | �糡ǿ�ȵķ�����ȵ����洹ֱ�������ɸߵĵ�����ָ��͵ĵ����� | |
| C�� | ���ŵ糡ǿ�ȵĴ�С��С������Ҳ���� | |
| D�� | ���κε糡�У�A��B ����ĵ��Ʋ� UAB��糡ǿ�� E��AB ��� d �Ĺ�ϵΪ��UAB=Ed |
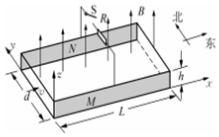 ��ͼ��ʾΪ���ú�������Ĵ����巢���ԭ��ʾ��ͼ�����η���ܵ�ˮƽ�������ã������ܵ����ڷ�����ֱ���ϣ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų��У����ϡ��������Ǿ�Ե�壬�ϡ���������M��N�ǵ���ɺ��Եĵ���壬��������뿪��S�Ͷ�ֵ����R��������֪����ܵ���ΪL����Ϊd����Ϊh����ˮ�ڷ���ܵ����Ժ㶨����v��������������������ܵ��ڵĺ�ˮ�ڴ�ֱ��������ĵ���Ϊr����ˮ�ڹܵ�������ʱ�ܵ�Ħ��������С��Ϊf�����Ƶشų���Ӱ�죬������
��ͼ��ʾΪ���ú�������Ĵ����巢���ԭ��ʾ��ͼ�����η���ܵ�ˮƽ�������ã������ܵ����ڷ�����ֱ���ϣ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų��У����ϡ��������Ǿ�Ե�壬�ϡ���������M��N�ǵ���ɺ��Եĵ���壬��������뿪��S�Ͷ�ֵ����R��������֪����ܵ���ΪL����Ϊd����Ϊh����ˮ�ڷ���ܵ����Ժ㶨����v��������������������ܵ��ڵĺ�ˮ�ڴ�ֱ��������ĵ���Ϊr����ˮ�ڹܵ�������ʱ�ܵ�Ħ��������С��Ϊf�����Ƶشų���Ӱ�죬������| A�� | ������N�ĵ��Ƹ� | |
| B�� | ����S�Ͽ�ʱ��M��N���˵ĵ�ѹΪBdv | |
| C�� | ����S�պ�ʱ������ܵ�������������ѹ����F=f+$\frac{{B}^{2}{d}^{2}{v}^{2}}{R+r}$ | |
| D�� | ����S�պ�ʱ������R�ϵĹ���Ϊ$\frac{{B}^{2}{d}^{2}{v}^{2}}{R}$ |
 һ�����������ѹ���ĵ�·��ͼ��ʾ������R1��R3��R4Ϊ��ֵ���裬R2Ϊ���������������Ϊ��������uΪ���ҽ�����Դ�������ѹ��Чֵ�㶨������ƬP�������һ����Ĺ����У�����˵����ȷ���ǣ�������
һ�����������ѹ���ĵ�·��ͼ��ʾ������R1��R3��R4Ϊ��ֵ���裬R2Ϊ���������������Ϊ��������uΪ���ҽ�����Դ�������ѹ��Чֵ�㶨������ƬP�������һ����Ĺ����У�����˵����ȷ���ǣ�������| A�� | ��ѹ��ʾ����� | B�� | ������C���������ʼ�ղ��� | ||
| C�� | ������ʾ����С | D�� | �����ѹ������������� |

| A�� | ����S�ɶϿ����պϵ�˲�� | |
| B�� | ��Դ�������Ӻ�S�ɱպϵ��Ͽ���˲�� | |
| C�� | ���ֿ���S�պϣ�������������ƬP�������һ��� | |
| D�� | ���ֿ���S�պϣ�������������ƬP�������һ��� |
 ��ͼ��ʾ�����費�Ƶ��������������Ϊl���̶���ˮƽ��Ե�����ϣ�б��MNPQ��ˮƽֱ�������͵����У�ˮƽֱ���첿�ִ��ڴŸ�Ӧǿ�ȴ�СΪB��������ֱ���µ���ǿ�ų��У�ĩ���������Եƽ�룬һ����Ϊm������ΪR�ĵ����ab�Ӿ�ˮƽ����ĸ߶�Ϊh�����ٶ��ͷţ�����ˮƽֱ����������˶�������뿪�����䵽ˮƽ�����ϣ���ص㵽�����Ե��ˮƽ����Ϊx����֪б����ˮƽ���ļн�Ϊ�ȣ�PM�����ӵ������ֵҲΪR���ҵ����abͨ���ų��Ĺ�����ͨ�����ĵ����Ϊq��������뵼��֮��Ķ�Ħ��������Ϊ�̣����������ĸ߶�ΪH���������ٶ�Ϊg����
��ͼ��ʾ�����費�Ƶ��������������Ϊl���̶���ˮƽ��Ե�����ϣ�б��MNPQ��ˮƽֱ�������͵����У�ˮƽֱ���첿�ִ��ڴŸ�Ӧǿ�ȴ�СΪB��������ֱ���µ���ǿ�ų��У�ĩ���������Եƽ�룬һ����Ϊm������ΪR�ĵ����ab�Ӿ�ˮƽ����ĸ߶�Ϊh�����ٶ��ͷţ�����ˮƽֱ����������˶�������뿪�����䵽ˮƽ�����ϣ���ص㵽�����Ե��ˮƽ����Ϊx����֪б����ˮƽ���ļн�Ϊ�ȣ�PM�����ӵ������ֵҲΪR���ҵ����abͨ���ų��Ĺ�����ͨ�����ĵ����Ϊq��������뵼��֮��Ķ�Ħ��������Ϊ�̣����������ĸ߶�ΪH���������ٶ�Ϊg����