题目内容
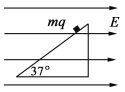
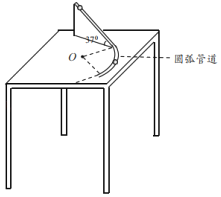
【题目】如图所示,边长为![]() m的正方形桌面距离水平地面的高度为0.8m,在桌面上固定一倾角为37°的斜面轨道,轨道底端与半径R=0.3m的水平放置光滑圆弧管道平滑连接,管道圆心位置与桌面中心O重合,管道弧长可调节。现从斜面轨道上距桌面高0.15m处由静止释放质量m=0.03kg的小滑块(可看做质点),滑块进入圆弧管道时的速度为
m的正方形桌面距离水平地面的高度为0.8m,在桌面上固定一倾角为37°的斜面轨道,轨道底端与半径R=0.3m的水平放置光滑圆弧管道平滑连接,管道圆心位置与桌面中心O重合,管道弧长可调节。现从斜面轨道上距桌面高0.15m处由静止释放质量m=0.03kg的小滑块(可看做质点),滑块进入圆弧管道时的速度为![]() m/s,离开管道后在桌面上继续向前运动,运动到桌面边缘后落到地面上。滑块运动过程中与倾斜轨道、水平桌面间的阻力均为其所受支持力的k倍,忽略管道本身大小及滑块在进出管道时速度的变化。已知sin37°=0.6,求:(结果可以保留根号)
m/s,离开管道后在桌面上继续向前运动,运动到桌面边缘后落到地面上。滑块运动过程中与倾斜轨道、水平桌面间的阻力均为其所受支持力的k倍,忽略管道本身大小及滑块在进出管道时速度的变化。已知sin37°=0.6,求:(结果可以保留根号)
(1)k的大小;
(2)圆弧管道对滑块的作用力大小;
(3)调节管道弧长,滑块离开管道后在桌面上运动的最长时间;
(4)调节管道弧长,滑块落地点与圆心O的水平距离的最大值。
【答案】(1)0.25(2)0.36N(3)0.57s(4)0.67m
【解析】
(1)匀加速过程的位移为:
![]()
末速度为:
![]()
根据匀变速直线运动的速度位移公式有:
![]()
根据牛顿第二定律有:
![]()
代入数据得:
![]()
(2)水平方向:
![]()
竖直方向上:
![]()
所以作用力
![]()
(3)滑块离开管道后在桌面上做匀减速直线运动,初速度为:
![]()
加速度大小为:
![]()
能滑行的最长时间为:
![]()
检验:当运动距离最长时对应的时间最长,分析知从桌角处滑行时有最长的运动距离,求得最长距离
![]()
匀减速运动的最大位移为:
![]()
比较知滑块运动到桌角处时速度恰好为零,上述结论成立;
(4)设滑块离开桌面时的速度大小为v2,在桌面运动的距离为
![]()
滑块在空中运动的时间为:t=0.4s,滑块在水平方向的距离为:
![]()
因此
![]()
当![]() 时,
时,![]()
根据勾股定理,落地点距离O点也最远,最远距离
![]()

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目