题目内容
【题目】在一倾角为![]() 的光滑绝缘斜面上方,有平行于斜面向上的匀强电场,虚线MN为电场的上边界,场强大小E=
的光滑绝缘斜面上方,有平行于斜面向上的匀强电场,虚线MN为电场的上边界,场强大小E=![]() V/m,MN上方有一长为L=0.5 m的轻质绝缘杆,杆的上下两端分别固定一个小球A、B(可看成质点),质量均为m=0.01 kg,A不带电,B带电荷量-q2=
V/m,MN上方有一长为L=0.5 m的轻质绝缘杆,杆的上下两端分别固定一个小球A、B(可看成质点),质量均为m=0.01 kg,A不带电,B带电荷量-q2=![]() C,B到MN的距离d=0.4 m.现将A、B两球由静止释放(g取10 m/s2),求:
C,B到MN的距离d=0.4 m.现将A、B两球由静止释放(g取10 m/s2),求:
(1)小球B在匀强电场中,而A还未进入电场时,两小球的加速度大小;
(2)从开始运动到A刚要进入匀强电场过程的时间。

【答案】(1)10m/s2 (2) 0.6 s
【解析】
(1)以A、B球以及杆整体做研究对象,由牛顿第二定律:
2mgsin30°+q2E =2ma
解得:a=10m/s2
(2)B未进入电场前,设系统的加速度为a1,时间为t1,由牛顿第二定律有
![]()
![]()
解得t1=0.4 s
B球进入电场瞬间的速度为
![]()
从B球进入电场至A球刚要进入电场,设这段时间为t2,由运动学公式
![]()
解得t2=0.2 s
从开始运动,至A球刚要进入电场的时间为
t=t1+t2=0.6 s.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
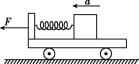
红果子三级测试卷系列答案【题目】如图1为用拉力传感器和速度传感器探究“加速度与物体受力的关系”实验装置.用拉力传感器记录小车受到拉力的大小,在长木板上相距L=48.0cm的A、B两点各安装一个速度传感器,分别记录小车到达A、B时的速率.

(1)实验主要步骤如下:
①将拉力传感器固定在小车上;
②平衡摩擦力,让小车做 运动;
③把细线的一端固定在拉力传感器上,另一端
通过定滑轮与钩码相连;
④接通电源后自C点释放小车,小车在细线拉动下运动,记录细线拉力F的大小及小车分别到达A、B时的速率vA、vB;
⑤改变所挂钩码的数量,重复④的操作.
(2)下表中记录了实验测得的几组数据,vB2﹣vA2是两个速度传感器记录速率的平方差,则加速度的表达式a= ,请将表中第3次的实验数据填写完整(结果保留三位有效数字);
次数 | F(N) | vB2﹣vA2(m2/s2) | a(m/s2) |
1 | 0.60 | 0.77 | 0.80 |
2 | 1.04 | 1.61 | 1.68 |
3 | 1.42 | 2.34 | |
4 | 2.62 | 4.65 | 4.84 |
5 | 3.00 | 5.49 | 5.72 |
(3)由表中数据,在图2坐标纸上作出a~F关系图线;
(4)对比实验结果与理论计算得到的关系图线(图中已画出理论图线),造成上述偏差的原因是 .