Question

【题目】一根轻质弹性绳的两端分别固定在水平天花板上相距80cm的两点上，弹性绳的原长也为80cm．将一钩码挂在弹性绳的中点，平衡时弹性绳的总长度为100cm；再将弹性绳的两端缓慢移至天花板上的同一点，则弹性绳的总长度变为（弹性绳的伸长始终处于弹性限度内）（　　）
A.86cm
B.92cm
C.98cm
D.104cm

Answer 1

【答案】B
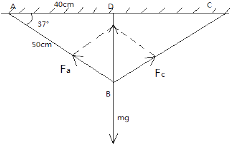
【解析】解：如图所示，绳子原长是80cm，伸长为100cm，如图，则AB段长50cm，伸长了10cm=0.1m，假设绳子的劲度系数为k，则绳子拉力为：

F=0.1k

把绳子的拉力分解为水平方向和竖直方向，在竖直方向的分量为：Fx=0.1k×cos53°=0.06k，

两个绳子的竖直方向拉力合力为：2Fx

物体处于平衡状态，则拉力合力等于重力，即为：0.12k=mg

解得：k=

当AC两点移动到同一点时，绳子两个绳子的夹角为0，每段绳子伸长x，则两个绳子的拉力合力为：

2kx=mg，

x=0.06m．

所以此时绳子总长度为92cm．

故答案为：B．

此题是物体的平衡问题，考查平行四边形定则的应用；在处理共点力平衡问题时，关键是对物体进行受力分析，然后根据正交分解法将各个力分解成两个方向上的力，然后列式求解，如果物体受到三力处于平衡状态，且两个力大小相等，则可根据矢量三角形法，将三个力移动到一个三角形中，然后根据角度列式求解。前后两次始终处于静止状态，即合外力为零，在改变绳长的同时，绳与竖直方向的夹角跟着改变。