题目内容
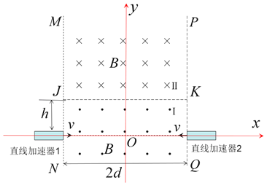
【题目】如图所示为一种研究高能粒子在不同位置对撞的装置。在关于y轴对称间距为2d的MN、PQ边界之间存在两个有界匀强磁场，其中K（K在x轴上方）下方I区域磁场垂直纸面向外，JK上方Ⅱ区域磁场垂直纸面向里，其磁感应强度均为B．直线加速器1与直线加速器2关于O点轴对称，其中心轴在位于x轴上，且末端刚好与MN、PQ的边界对齐；质量为m、电荷量为e的正、负电子通过直线加速器加速后同时以相同速率垂直MN、PQ边界进入磁场。为实现正、负电子在Ⅱ区域的y轴上实现对心碰撞（速度方向刚好相反），根据入射速度的变化，可调节边界与x轴之间的距离h，不计粒子间的相互作用，不计正、负电子的重力，求：
（1）哪个直线加速器加速的是正电子；
（2）正、负电子同时以相同速度ν1进入磁场，仅经过边界一次，然后在Ⅱ区域发生对心碰撞，试通过计算求出v1的最小值。
（3）正、负电子同时以v2
速度进入磁场，求正、负电子在Ⅱ区域y轴上发生对心碰撞的位置离O点的距离。
【答案】（1）直线加速器2（2）
；（3）△y＝2[
]，n＝1，3，5，7…2k﹣1。
【解析】
（1）正负电子进入磁场后要在Ⅱ区域相遇，因此正负电子出加速器以后都向上偏转，根据左手定则可知直线加速器2加速得为正电子
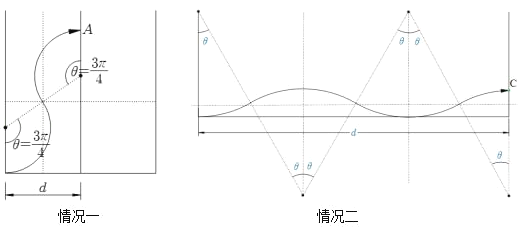
（2）如图所示：d＝2Rsinθ，R（1﹣cosθ）＝h
或直接得：
整理得：R
即当
，即h
时，Rmin
根据ev1B＝m
，求得：v1
（3）当v
，则R
，距离总是满足：△y＝2h
情况一：h＞R，只有一种情况h＝R
，△y
情况二：h＜R，
，h＝R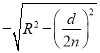
，
那么△y＝2[
]，n＝1，3，5，7…2k﹣1
练习册系列答案
相关题目
