��Ŀ����
����Ŀ����ͼ��ʾ������ֱƽ�����й��ABC������AB��Ϊˮƽֱ�����������m=0.5kg��С��飨����Ϊ�ʵ㣩֮��Ķ�Ħ��������=0.2��BC��Ϊ�⻬��Բ�ι��������뾶R=2m�����AB��BC��B�����У�С�����ˮƽ����F=3N�������´�A���ɾ�ֹ��ʼ���ȼ���ֱ���˶�������Բ���������͵�Bʱ��ȥ��������ʱ�ٶ�vB=10m/s��ȡg=10m/s2 �� ��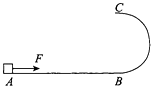
��1������F���˶��ٹ���
��2������B���˲�䣬���Թ����ѹ���Ƕ��
��3����������ߵ�C�ɳ����䵽ˮƽ����ϵ�D�㣨ͼ��δ����������BD��ľ��룮
���𰸡�
��1���⣺�����ˮƽ�����˶�ʱ����ţ�ٵڶ����ɵã�
F����mg=ma
��� a=4m/s2��
��AB��ľ��� SAB= ![]() =12.5m
=12.5m
����F���� W=FSAB=37.5J
������F����37.5J����
��2���⣺��ţ�ٵڶ����� N��mg=m ![]()
��� N=30N
��ţ�ٵ������ɵ����Թ����ѹ�� N��=N=30N
�𣺾���B���˲�䣬���Թ����ѹ����30N��
��3���⣺��B��C�Ĺ��̣��ɻ�е���غ㶨�ɵ�
2mgR+ ![]() =
= ![]()
����뿪C�����ƽ���˶�����
2R= ![]()
x=vCt
�������ݽ�� x=4m
��BD��ľ�����4m��
����������1���о������ˮƽ�����˶��Ĺ��̣�����ţ�ٵڶ�����������ٶȣ����ٶ�λ�ƹ�ϵ��ʽ���AB��ľ��룬���ɹ��ļ��㹫ʽ��⣮��2����B�㣬��ţ�ٵڶ�����������������֧����������ţ�ٵ������������Թ����ѹ������3������B��C�����û�е���غ㶨��������ͨ��C����ٶȣ�����ƽ���˶��Ĺ�����BD��ľ��룮
�����㾫�����������⣬������Ҫ�˽�ƽ���˶�(�ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶�)����Ҫ���ջ�е���غ㼰������(��ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ���)�����֪ʶ���Ǵ���Ĺؼ���

 �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д� ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д�