题目内容
已知月球绕地球运动周期T和轨道半径r,地球半径为R,万有引力常量为G.则地球的质量为 ,地球的平均密度为 。
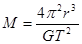
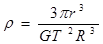
解析试题分析:地球对月球的万有引力充当向心力,,所以根据万有引力定律以及牛顿第二定律可得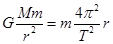 ,解得:
,解得: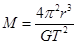 ,地球的体积
,地球的体积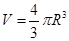 ,,根据
,,根据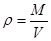 可得
可得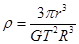
考点:考查了万有引力定律的应用
点评:基础题,关键对公式的灵活应用,计算时需要细心

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
地球“空间站”正在地球赤道平面内的圆周轨道上运动,其离地高度为同步卫星离地高度的十分之一,且运行方向与地球自转方向相同,则关于该“空间站”的说法正确的是
| A.运行速度大于同步卫星的运行速度 |
| B.运行周期大于地球自转周期 |
| C.站在地球赤道上的人看到它向东运动 |
| D.在“空间站”里面的工作人员处于平衡状态 |
质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的( )
A.线速度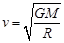 | B.角速度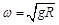 |
C.运行周期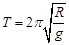 | D.向心加速度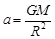 |
一艘宇宙飞船飞近某一新发现的行星,并进入该行星表面的圆形轨道绕行数圈后,着陆在该行星上。飞船上备有以下器材:
| A.秒表一只 | B.质量为m的物体一个 |
| C.弹簧测力计一个 | D.天平一架(带砝码) |
(1)绕行时需测量的物理量为 __,选用的器材是 _________(填序号)
(2)着陆后需测量的物理量为_______,选用的器材是 ________(填序号)
(3)利用测得的物理量写出半径R= _________,质量M=________
 ;
;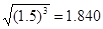 ;
;