题目内容
7.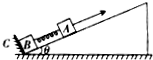 在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度方向沿斜面向上,大小为a,则( )
在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度方向沿斜面向上,大小为a,则( )| A. | 从静止到B刚离开C的过程中,A发生的位移为$\frac{3mgsinθ}{k}$ | |
| B. | 从静止到B刚离开C的过程中,重力对A做的功为-$\frac{3{m}^{2}{g}^{2}sinθ}{k}$ | |
| C. | B刚离开C时,恒力对A做功的功率为(mgsinθ+ma)v | |
| D. | 当A的速度达到最大时,B的加速度大小为$\frac{a}{2}$ |
分析 未加拉力F时,物体A对弹簧的压力等于其重力的下滑分力;物块B刚要离开C时,弹簧的拉力等于物体B重力的下滑分力;根据平衡条件并结合胡克定律求解出两个状态弹簧的形变量,得到弹簧的长度变化情况;然后结合功能关系进行分析即可
解答 解:A、开始时,弹簧处于压缩状态,压力等于物体A重力的下滑分力,根据胡克定律,有:
mgsinθ=kx1
解得:x1=$\frac{mgsinθ}{k}$
物块B刚要离开C时,弹簧的拉力等于物体B重力的下滑分力,根据胡克定律,有;
2mgsinθ=kx2
解得:x2=$\frac{2mgsinθ}{k}$
故物块A运动的距离为:$△x={x}_{1}-{x}_{2}=\frac{3mgsinθ}{k}$,故A正确;
B、从静止到B刚离开C的过程中,物块A克服重力做功为$W=mg•△x•sinx=\frac{3{m}^{2}{g}^{2}si{n}^{2}θ}{k}$,故B错误;
C、此时物体A受拉力、重力、支持力和弹簧的拉力,根据牛顿第二定律,有:
F-mgsinθ-T=ma
弹簧的拉力等于物体B重力的下滑分力,为:
T=2mgsinθ
故:F=3mgsinθ+ma,恒力对A做功的功率为(3mgsinθ+ma)v.故C错误;
D、当A的速度达到最大时,A受到的合外力为0,则:F-mgsinθ-T′=0
所以:T′=2mgsinθ+ma
B沿斜面方向受到的力:FB=T′-2mgsinθ=ma
又:FB=2ma′
所以:$a′=\frac{{F}_{B}}{2m}=\frac{ma}{2m}=\frac{a}{2}$.故D正确.
故选:AD
点评 本题关键抓住两个临界状态,开始时的平衡状态和最后的B物体恰好要滑动的临界状态,然后结合功能关系分析,难度适中

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
18.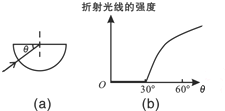 一束红色的细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示.下列说法正确的是( )
一束红色的细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示.下列说法正确的是( )
 一束红色的细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示.下列说法正确的是( )
一束红色的细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示.下列说法正确的是( )| A. | 透明体对红光的折射率为$\frac{2\sqrt{3}}{3}$ | |
| B. | 红光在透明体中的速度大小与在真空中的相同 | |
| C. | 红光的折射光线的频率会随着折射光线强度的增大而增大 | |
| D. | 红光在透明体内发生全反射的临界角为30° |
15.汽车发动机的功率为60kW,若其总质量为5t,在水平路面上行驶时,所受阻力恒定为5.0×103N,试求:
(1)当汽车加速度为2m/s2时,速度为多大;
(2)当汽车速度为6m/s时,加速度为多大.
(1)当汽车加速度为2m/s2时,速度为多大;
(2)当汽车速度为6m/s时,加速度为多大.
12.跳水比赛是我国的传统优势项目,运动员进行10m跳台比赛时,不计空气阻力,在空中运动时下列说法正确的是( )
| A. | 为了研究运动员的技术动作,可将正在比赛的运动员视为质点 | |
| B. | 运动员在下落过程中,会感觉到水面在匀加速上升 | |
| C. | 前一半位移用的时间短,后一半位移用的时间长 | |
| D. | 前一半时间内位移大,后一半时间内位移小 |
19.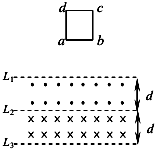 如图所示,相距均为d的三条水平虚线L1与L2、L2与L3之间分别有垂直纸面向外、向里的匀强磁场,磁感应强度大小均为B.一个边长也是d的正方形导线框,从L1上方一定高处由静止开始自由下落,当ab边刚越过L1进入磁场时,恰好以速度v1做匀速直线运动;当ab边在越过L2运动到L3之前的某个时刻,线框又开始以速度v2做匀速直线运动,在线框从进入磁场到速度变为v2的过程中,设线框的动能变化量大小为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,该过程导线框中产生的电能大小为E0,下列说法中正确的是( )
如图所示,相距均为d的三条水平虚线L1与L2、L2与L3之间分别有垂直纸面向外、向里的匀强磁场,磁感应强度大小均为B.一个边长也是d的正方形导线框,从L1上方一定高处由静止开始自由下落,当ab边刚越过L1进入磁场时,恰好以速度v1做匀速直线运动;当ab边在越过L2运动到L3之前的某个时刻,线框又开始以速度v2做匀速直线运动,在线框从进入磁场到速度变为v2的过程中,设线框的动能变化量大小为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,该过程导线框中产生的电能大小为E0,下列说法中正确的是( )
 如图所示,相距均为d的三条水平虚线L1与L2、L2与L3之间分别有垂直纸面向外、向里的匀强磁场,磁感应强度大小均为B.一个边长也是d的正方形导线框,从L1上方一定高处由静止开始自由下落,当ab边刚越过L1进入磁场时,恰好以速度v1做匀速直线运动;当ab边在越过L2运动到L3之前的某个时刻,线框又开始以速度v2做匀速直线运动,在线框从进入磁场到速度变为v2的过程中,设线框的动能变化量大小为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,该过程导线框中产生的电能大小为E0,下列说法中正确的是( )
如图所示,相距均为d的三条水平虚线L1与L2、L2与L3之间分别有垂直纸面向外、向里的匀强磁场,磁感应强度大小均为B.一个边长也是d的正方形导线框,从L1上方一定高处由静止开始自由下落,当ab边刚越过L1进入磁场时,恰好以速度v1做匀速直线运动;当ab边在越过L2运动到L3之前的某个时刻,线框又开始以速度v2做匀速直线运动,在线框从进入磁场到速度变为v2的过程中,设线框的动能变化量大小为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,该过程导线框中产生的电能大小为E0,下列说法中正确的是( )| A. | 在导线框下落过程中,由于重力做正功,所以有v2>v1 | |
| B. | 该过程中线框动能的变化量大小为△Ek=W2-W1-E0 | |
| C. | 该过程中线框中的电流方向没有发生变化 | |
| D. | 在导线框通过磁场的整个过程中,线框中的平均感应电流为零 |
16.用单色光照射某种金属表面发生光电效应.已知单色光的频率为v,金属的逸出功为W,普朗克常数为k,光电子的最大初动能为Ek,下列关于它们之间关系的表达式正确的是( )
| A. | Ek=hv-W | B. | Ek=hv+W | C. | W=Ek-hv | D. | W=Ek+hv |
17.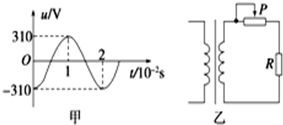 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )
 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )| A. | 原线圈的电压瞬时表达式为u=310sin100πt | |
| B. | 副线圈输出电压的有效值为22V | |
| C. | P向右移动时,原、副线圈的电流比减小 | |
| D. | P向右移动时,变压器的输入功率减少 |
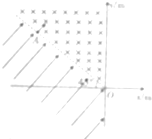 如图所示,空间中第二、三象限存在电、磁场区域,以45°线为分界线,匀强磁场方向垂直于纸面向里,匀强电场方向垂直于分界线向上,一带负电的离子在分界线上的A点以一定速度射入磁场区域,其轨迹在半个周期内恰与y轴相切,已知A到原点O的距离为(1+$\sqrt{2}$)m,该负离子的比荷$\frac{q}{m}$=107C/kg,磁场的磁感应强度大小B=0.4T,电场强度大小E=$\frac{\sqrt{2}+1}{5}$×108V/m.
如图所示,空间中第二、三象限存在电、磁场区域,以45°线为分界线,匀强磁场方向垂直于纸面向里,匀强电场方向垂直于分界线向上,一带负电的离子在分界线上的A点以一定速度射入磁场区域,其轨迹在半个周期内恰与y轴相切,已知A到原点O的距离为(1+$\sqrt{2}$)m,该负离子的比荷$\frac{q}{m}$=107C/kg,磁场的磁感应强度大小B=0.4T,电场强度大小E=$\frac{\sqrt{2}+1}{5}$×108V/m.