题目内容
18.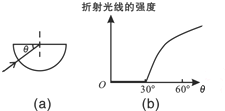 一束红色的细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示.下列说法正确的是( )
一束红色的细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示.下列说法正确的是( )| A. | 透明体对红光的折射率为$\frac{2\sqrt{3}}{3}$ | |
| B. | 红光在透明体中的速度大小与在真空中的相同 | |
| C. | 红光的折射光线的频率会随着折射光线强度的增大而增大 | |
| D. | 红光在透明体内发生全反射的临界角为30° |
分析 AD、由图b得到全反射临界角为60°,根据sinC=$\frac{1}{n}$求解折射率;
B、根据c=nv判断红光在透明体中的速度大小;
C、光线的频率与介质的折射率无关.
解答 解:AD、由图b得到θ=30°时发生全反射,故全反射的临界角C=60°,故:
n=$\frac{1}{sinC}=\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2}{3}\sqrt{3}$;故A正确,D错误;
B、根据v=$\frac{c}{n}$,红光在透明体中的光速小于真空中的光速,故B错误;
C、光线的频率与介质的折射率无关,故红光的折射光线的频率不变,故C错误;
故选:A.
点评 本题关键是由图b得到全反射的临界角,然后结合公式sinC=$\frac{1}{n}$和v=$\frac{c}{n}$进行分析,基础题目.

练习册系列答案
相关题目
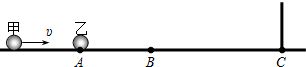
7.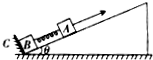 在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度方向沿斜面向上,大小为a,则( )
在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度方向沿斜面向上,大小为a,则( )
 在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度方向沿斜面向上,大小为a,则( )
在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度方向沿斜面向上,大小为a,则( )| A. | 从静止到B刚离开C的过程中,A发生的位移为$\frac{3mgsinθ}{k}$ | |
| B. | 从静止到B刚离开C的过程中,重力对A做的功为-$\frac{3{m}^{2}{g}^{2}sinθ}{k}$ | |
| C. | B刚离开C时,恒力对A做功的功率为(mgsinθ+ma)v | |
| D. | 当A的速度达到最大时,B的加速度大小为$\frac{a}{2}$ |
8.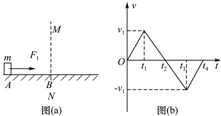 静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )
静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )
 静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )
静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )| A. | 在B点的右边加速度大小为$\frac{v_1}{{{t_2}-{t_1}}}$ | |
| B. | 小物块在经过B点后向右运动的时间为t3-t1 | |
| C. | F2的大小为$\frac{{m{v_1}}}{{{t_2}-{t_1}}}$ | |
| D. | 小物块在B点右边运动的最大距离为$\frac{{v}_{1}{t}_{2}}{2}$ |
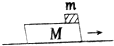 如图所示,在光滑水平面上,有一质量为M的长木块以一定的初速度向右匀速运动,将质量为m的小铁块无初速度地请放在木块右端,小铁块与木块间的动摩擦因数为μ,当小铁块在木块上相对木块滑动L时与木块保持相对静止,此时长木块对地位移为l,求这个过程中:
如图所示,在光滑水平面上,有一质量为M的长木块以一定的初速度向右匀速运动,将质量为m的小铁块无初速度地请放在木块右端,小铁块与木块间的动摩擦因数为μ,当小铁块在木块上相对木块滑动L时与木块保持相对静止,此时长木块对地位移为l,求这个过程中: 光滑水平面上有四个静止的小木块A和B,其质量mA=mB=1kg,它们中间用一根轻质弹簧相连,一颗质量为m=50g水平飞行的子弹以v0=500m/s的速度在极短的时间内射穿两木块.已知射穿A木块后子弹的速度变为v1=300m/s,射穿B木板后子弹的速度变为v2=200m/s,求系统运动过程中弹簧第一次恢复到原长时,小木块A、B的速度大小.
光滑水平面上有四个静止的小木块A和B,其质量mA=mB=1kg,它们中间用一根轻质弹簧相连,一颗质量为m=50g水平飞行的子弹以v0=500m/s的速度在极短的时间内射穿两木块.已知射穿A木块后子弹的速度变为v1=300m/s,射穿B木板后子弹的速度变为v2=200m/s,求系统运动过程中弹簧第一次恢复到原长时,小木块A、B的速度大小.