题目内容
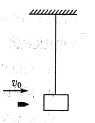
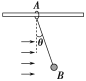
【题目】如图所示,一辆小车静止在水平地面上,车内固定着一个倾角为60°的光滑斜面OA,光滑挡板OB与水平方向的夹角为θ,挡板OB可绕转轴O在竖直平面内转动。现将重为G的圆球放在斜面与挡板之间。下列说法正确的是( )
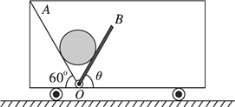
A. 若θ=60°,球对斜面的压力大小为G
B. 若挡板OB从θ=30°位置沿逆时针方向缓慢转动到θ=90°过程中,则球对斜面的压力逐渐增大
C. 若θ=30°,使小车水平向左做变加速运动,则小车对地面的压力增大
D. 若θ=60°,使小车水平向右做匀加速直线运动,则球对挡板的压力可能为零
【答案】ABD
【解析】
以球为研究对象,对球进行受力分析,根据牛顿第二定律或平衡条件求出挡板对球的作用力;
若挡板旋转,分析小球受力情况,作出力图,运用图解法,分析支持力的变化情况即可;
A、若![]() ,球处于静止状态,受力平衡,对球进行受力分析,如图所示:
,球处于静止状态,受力平衡,对球进行受力分析,如图所示:

![]() 为邻边作平行四边形,根据几何关系可知,
为邻边作平行四边形,根据几何关系可知,![]() ,由牛顿第三定律知,球对斜面的压力大小为G,故A正确;
,由牛顿第三定律知,球对斜面的压力大小为G,故A正确;
B、若挡板从![]() 位置沿逆时针方向缓慢转动到
位置沿逆时针方向缓慢转动到![]() 过程中,
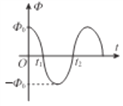
过程中,![]() 的方向始终不变,根据图象可知,
的方向始终不变,根据图象可知,![]() 都增大,根据牛顿第三定律可知,球对斜面的压力增大,故B正确;
都增大,根据牛顿第三定律可知,球对斜面的压力增大,故B正确;
C、整体在水平方向有加速度,但是竖直方向没有运动,即竖直方向的合力为零,根据平衡条件可知地面对小车整体的支持力等于小车整体的重力,根据牛顿第三定律可知,小车整体对地面的压力大小等于小车整体的重力,故选项C错误;
D、若保持挡板不动,使小车水平向右做匀加速直线运动,当![]() 和重力G的合力正好提供产生加速度时的力时,球对挡板的压力为零,故D正确。
和重力G的合力正好提供产生加速度时的力时,球对挡板的压力为零,故D正确。

 愉快的寒假南京出版社系列答案
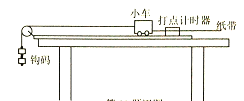
愉快的寒假南京出版社系列答案【题目】某小组利用如图甲所示的装置验证牛顿第二定律.实验中,他们平衡了摩擦力,用天平测出小车的总质量,用细线所挂钩码的总重代替小车所受的牵引力大小F.
(1)他们还在实验时调节木板上定滑轮的高度,使牵引小车的细线与木板平行.这样做的目的是_________.
A.避免小车在运动过程中发生抖动
B.使打点计时器在纸带上打出的点迹清晰
C.保证小车最终能够做匀速直线运动
D.使细线拉力等于小车受到的合力
(2)实验得到一条点迹清晰的纸带如图乙所示,O、A、B、C、D是在纸带上选取的计数点,相邻计数点间还有4个打的点未画出,AB、CD间的距离分别为x1、x2,打点计时器的打点周期为T,则小车运动的加速度大小为________.
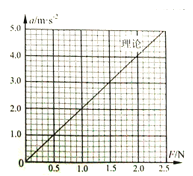
(3)下表录了小车质量一定时,牵引力大小F与对应的加速度a的几组数据,请在图丙的坐标中描点作出a-F图线.
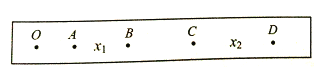
钩码个数 | 1 | 2 | 3 | 4 | 5 |
F(N) | 0.49 | 0.98 | 1.47 | 1.96 | 2.45 |
a(m·s-2) | 0.92 | 1.68 | 2.32 | 2.88 | 3.32 |
(4)实验中画出的a-F图线与理论计算的图线(图中已画出)有明显偏差,其原因主要是________________.