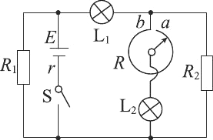
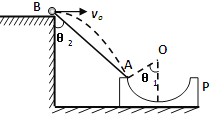
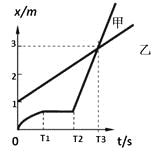
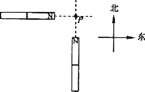
��Ŀ����
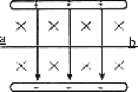
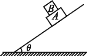
����Ŀ��(��ѡ)����������һ��Ļ������ڹ̶��ġ����Ϊ����б����,��ͼ��ʾ,����A��B�������ֱ�ΪM��m,A��б���Ķ�Ħ������Ϊ��1,B��A֮��Ķ�Ħ������Ϊ��2,�������ٶ�Ϊg,��֪�����鶼�Ӿ�ֹ��ʼ����ͬ�ļ��ٶ���б�滬��,����B�ܵ���Ħ���� (����)
A. ������ B. �����������
C. ��С������1mgcos �� D. ���ڵ�����2mgcos ��
���𰸡�BC
��������
�⣺��A��B��������������ͼ��ʾ��
����б�淽����ţ�ٵڶ����ɵã�
��m+M��gsin�ȩ�F=��m+M��a ��
�һ���Ħ����F=��1��m+M��gcos�� ��
���٢���a=g��sin�ȩ���1cos����
����A�ܵ�Ħ����FA������б�����£�A��������B��֧������Ħ����
����б�淽������ţ�ٵڶ����ɵã�mgsin��+FA=ma����
��������ʽ���FA=����1mgcos����
���ű�ʾFA���������ķ����෴����B��A��Ħ������б�����ϣ�
����ţ�ٵ������ɣ�A��B��Ħ����������б�����£���C��ȷ�� ��A��B��D����
��ѡ��C

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ