题目内容
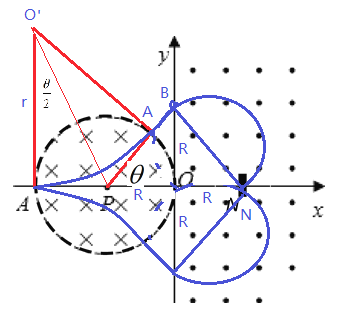
【题目】如图所示，在y轴左侧有半径为R的圆形边界匀强磁场，其圆心为x轴上的P点，磁感应强度大小为B，方向垂直于纸面向里。y轴右侧有垂直于纸面向外的匀强磁场，磁感应强度为
，两磁场的边界相切于O点。在磁场中距离O点右侧R的N点处有一个厚度忽略不计，宽度很窄的挡板，粒子与该挡板碰撞后速度大小不变，反弹后的角度与碰撞前相同（类似光的反射）。现一质量为m，带电量为＋q的粒子从A点以速度v，（大小未知）沿着x轴正方向射入磁场，经过一段时间后射离圆形边界的磁场，其速度方向偏离原来方向的夹角为45°．忽略重力和空气阻力。求：
（1）粒子从A出发到第一次离开圆形边界磁场所用的时间；
（2）粒子能否再回到A点，若不能，说明理由；若能，求从A点出发到回到A点所用的时间。
【答案】（1）
（2）
【解析】
由题意画出运动轨迹图，并由几何关系来确定圆心角，写出周期公式，寻找每次旋转后角度变化规律来来计算各段时间，然后求出求总时间；
（1）带电粒子在左边圆形磁场内运动如图所示，设
，则粒子圆周运动的圆心角也为
，则粒子从A出发到第一次离开圆形边界磁场所用的时间为：
；
（2）由图可知，在左侧磁场中有：
，
而且：
则：
由图可知粒子从左侧磁场飞出进入右边磁场，中间AB段没有磁场作用，为匀速运动，根据几何关系可知：
则在AB段时间为：
在右侧磁场中运动：
整理可以得到：
，可知在右边的运动为两个半圆
这两个半圆的总时间为：
由图可知，粒子仍能回到A点，则从A点出发到回到A点所用的时间为：
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
