题目内容
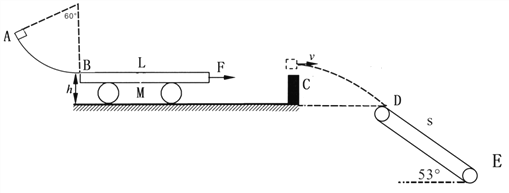
【题目】如图所示，AB为光滑圆弧轨道，半径R=2.5m，圆心角为60°，质量M=4kg
的小车（紧靠B点）静止在光滑水平面上，上表面离地高度h=0.8m，且与B点的等
高，右侧很远处有一个和小车等高的障碍物C（厚度可忽略），DE是以恒定速率15m/s
转动的传送带，D点位于水平面上。有一可视为质点m=1kg的物块，从A点静止释
放，在B点冲上小车时，小车立即受到一水平向右恒力F的作用。当物块滑到小车
最右端时，二者恰好相对静止，同时撤掉恒力F，然后小车撞到障碍物C后立即停止
运动，物块沿水平方向飞出，在D点恰好无碰撞地切入传送带，并沿着传送带下滑。
已知物块与小车间的动摩擦因数μ1=0.2，与传送带的动摩擦因数为μ2=
，传送带长
度为s=28m，与水平面的夹角为53°（取g=10m/s2，sin53°=0.8，cos53°=0.6）。求：
（1）物块滑到B点的速度大小v0和物块飞离小车的水平速度大小v；
（2）恒力F的大小和小车的长度L；
（3）物块在传送带上的运动时间t及在传送带上由于摩擦产生的内能Q。
【答案】（1）
（2）
（3）①若传送带顺时针转动, 
..
【解析】试题分析：由机械能守恒定律求出物块滑到B点的速度大小v0，研究小车撞到障碍物C后物块沿水平方向飞出的过程，该过程物块做平抛运动，下落的高度为h，到达D点时速度与水平方向的夹角为53°，由h求得下落到D点时竖直分速度，再由速度分解法求得物块飞离小车的水平速度大小v和物块滑到B点的速度大小v0；物块在小车上运动的过程中做匀减速运动，由速度时间公式求出物块在小车上滑行的时间．再对小车，由牛顿第二定律和速度公式结合求F，由位移公式求出物块与小车的位移，两者之差即等于小车的长度L；分析物块在传送带上的运动情况，由牛顿第二定律和运动学公式求时间t，求得两者的相对位移，即可求得内能Q。
（1）对物块， 从A到B根据动能定理： 
带入数据解得： 
以物块为研究对象在平抛过程： 
在D点沿切线飞入速度关系为： 
带入数据解得：v=3m/s
（2）以物块为研究对象，由牛顿第二定律得： 
带入数据解得：a1=2m/s2
对小车，由牛顿第二定律得： 
设经过时间t1物块与小车相对静止
由
， 带入数据解得：a2 =3 m/s2
解得：F=10N .
物块与小车在时间t1内通过的位移分别为： 
则小车的长度为：L=x1-x2=2.5m
（3）①若传送带顺时针转动，传送带速度v3=15m/s，由题意知：摩擦力f=μ2mgcos53°=2N，
重力沿斜面的分量mgsin53°=8N且有f< mgsin53°，可知物块与传送带速度相同后仍将继续加速下滑，速度相等前， 
物块到达D点的速：v2=v/cos530=5m/s
由速度v3= v2+ a3 t3，解得t3=1s
根据位移时间关系： 
带入数据解得：s1=10m
产生的热量为：Q1=f(v3 t3- s1)
带入数据解得：Q1=10J
速度相等后，由牛顿第二定律可得：span> 
解得：a4 =6m/s2
位移关系为：s2=s- s1=18m
由位移关系为： 
带入数据解得：t4=1s，其中t4=-6s（舍去）
该过程产生的热量为： 
所以：t= t3+ t4=2s 产生的总内能为：Q= Q1 +Q2=16J
②若传送带逆时针转动，物块一直下滑，时间为t5
位移时间关系为： 
解得： 
，其中t5=-4s(舍去)
所以产生的热量为： 
