Question

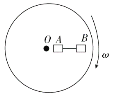
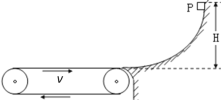
【题目】如图所示，一条足够长水平方向上的传送带以恒定速度v=3m/s沿顺时针方向转动，传送带右端固定一光滑曲面，并与曲面水平相切。质量m=1kg的物块自曲面上H=0.8m高处的P点由静止滑下，滑到传送带上继续向左运动。已知物块与传送带间的动摩擦因数为μ=0.2，不计物块滑过曲面与传送带交接处的能量损失，求：

（1）物块沿曲面返回时上升的最大高度。

（2）物块第一次在带上滑动时产生的热量

Answer 1

【答案】(1)0.45m (2)

【解析】

(1)物体由静止滑下第一次到达传送带右端根据动能定理有：

解得v1 = 4m/s.

接着物块向左减速到0，摩擦力提供加速度有：

减速到0的时间有：

向左运动的距离：

接着物块向右加速最大位移：

，所以物块一直向右加速到3m/s，然后匀速到传送带最右端.

设物块第一次上升的最大高度h，则：

代入数据解得h=0.45m

(2)设物块第一次在传送带上运动产生的焦耳热为Q,则根据能量关系有：

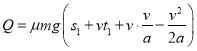
带入数据解得：

答：（1）物块沿曲面返回时上升的最大高度h=0.45m。

（2）物块第一次在带上滑动时产生的热量