题目内容
【题目】如图所示,细线上吊着小球,用水平恒力F将它从静止开始从竖直位置A拉到位置B,小球在B点受到的沿圆弧切线方向的合力恰好为零,此时线与竖直方向的夹角为θ,则有:
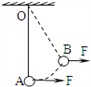
A. 恒力F做的功大于小球重力势能的增量
B. 小球将静止在B点
C. 细线对小球做的功为零
D. 若在B点将力F撤去,小球来回摆动的角度将大于θ
【答案】ACD
【解析】由A到B的过程中恒力F做功,使得小球的动能和重力势能均增加,故根据功能关系得知,恒力F做的功大于小球势能的增量,故A正确;由题意,小球在B点受到的沿圆弧切线方向的合力恰好为零,即拉力F与重力沿圆弧切线方向的分力大小相等、方向相反,则到达B点之前,小球在B点受到的沿圆弧切线方向的合力大于零,方向与速度方向相同,故从A到B小球做加速运动,故小球不可能静止在B点,故B错误;细线的拉力始终与速度方向垂直,所以不做功,故C正确;若在B点将力F撤去时,由于存在速度,所以小球来回摆动时偏离竖直方向的最大角度大于θ,故D正确。所以ACD正确,C错误。

练习册系列答案
相关题目


