题目内容
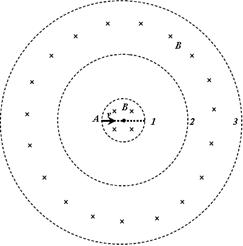
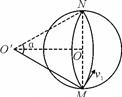
如图所示,半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁场方向垂直于纸面向里,匀强磁场的磁感应强度为B,圆筒形场区的边界由弹性材料构成。一个质量为m.电荷量为q的正离子(不计重力)以某一速度从筒壁上的小孔M进入筒中,速度方向与半径成θ=30°夹角,并垂直于磁场方向。离子和筒壁的碰撞无能量和电荷量的损失.若选择合适的进入速度,离子可以从M孔射出。问:

(1)离子的速度多大时,离子可以在最短的时间内返回M孔最短的时间是多少?
(2)如果离子与筒壁发生两次碰撞后从M孔射出,离子的速率是多大?从进入圆筒到返回M孔经历的时间是多少?

(1)离子的速度多大时,离子可以在最短的时间内返回M孔最短的时间是多少?
(2)如果离子与筒壁发生两次碰撞后从M孔射出,离子的速率是多大?从进入圆筒到返回M孔经历的时间是多少?
(1) 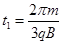 (2)
(2)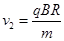
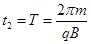
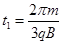 (2)
(2)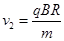
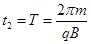
(1)离子要在最短的时间内返回M孔,离子只能与圆筒碰撞一次,据此画出离子的运动轨迹如图所示,碰撞点在过M点的直径的另一端N。设离子在磁场中的轨迹半径为r,速率为V1.根据向心力公式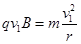 ,①结合图中的几何关系可得r=2R,②解得离子的速率
,①结合图中的几何关系可得r=2R,②解得离子的速率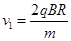 ,③离子在磁场中走过的每段圆弧对应的圆心角
,③离子在磁场中走过的每段圆弧对应的圆心角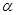 =60°,④经历的时间
=60°,④经历的时间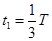 ,⑤即
,⑤即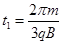 .⑥
.⑥
(2)离子与筒壁发生两次碰撞后从M孔射出,根据对称性画出离子的运动轨迹如图所示。
结合图中的几何关系可得r=R, ⑦
则离子的速率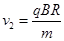 , ⑧
, ⑧
离子在磁场中走过的每段圆弧对应的圆心角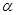 ′=120°, ⑨
′=120°, ⑨
经历的时间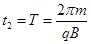 。 ⑩
。 ⑩
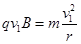 ,①结合图中的几何关系可得r=2R,②解得离子的速率
,①结合图中的几何关系可得r=2R,②解得离子的速率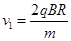 ,③离子在磁场中走过的每段圆弧对应的圆心角
,③离子在磁场中走过的每段圆弧对应的圆心角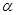 =60°,④经历的时间
=60°,④经历的时间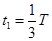 ,⑤即
,⑤即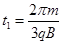 .⑥
.⑥(2)离子与筒壁发生两次碰撞后从M孔射出,根据对称性画出离子的运动轨迹如图所示。
结合图中的几何关系可得r=R, ⑦
则离子的速率
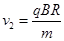 , ⑧
, ⑧离子在磁场中走过的每段圆弧对应的圆心角
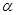 ′=120°, ⑨
′=120°, ⑨经历的时间
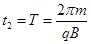 。 ⑩
。 ⑩


练习册系列答案
相关题目



 之比是
之比是

 cm
cm cm≤y≤
cm≤y≤

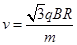 飞进圆1内部磁场。问:
飞进圆1内部磁场。问: