题目内容
【题目】如图甲所示,一长为l=1m的轻绳,一端穿在过O点的水平转轴上,另一端固定一质量为m的小球,整个装置绕O点在竖直面内转动.给系统输入能量,使小球通过最高点的速度不断加快,通过传感器测得小球通过最高点时,绳对小球的拉力F与小球在最高点动能Ek的关系如图乙所示,重力加速度为g,不考虑摩擦和空气阻力,请分析并回答以下问题: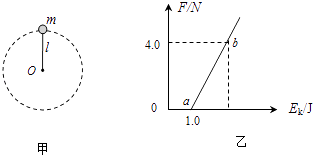
(1)若要小球能做完整的圆周运动,对小球过最高点的速度有何要求?(用题中给出的字母表示).
(2)请根据题目及图象中的条件求出小球质量m的值.(g取10m/s2)
(3)求小球从图中a点所示状态到图中b点所示状态的过程中,外界对此系统做的功.
(4)当小球达到图乙中b点所示状态时,立刻停止能量输入.之后的运动过程中,在绳中拉力达到最大值的位置,轻绳绷断,求绷断瞬间绳中拉力的大小.
【答案】
(1)解:小球刚好通过最高点做完整圆运动要求在最高点受力满足:mg=m ![]() ,
,
因此小球过最高点的速度要满足:v≥ ![]()
答:若要小球能做完整的圆周运动,对小球过最高点的速度满足:v≥ ![]()
(2)解:小球在最高点时有:mg+F=m ![]() 又因为:EK=
又因为:EK= ![]() mv2,
mv2,
所以绳对小球的拉力F与小球在最高点动能Ek的关系式为:F= ![]() ﹣mg,
﹣mg,
由图象知,当EK=1.0J时,F=0,代入上式得到:mgl=2.0J;又已知l=1m,则小球的质量m=0.2kg.
答:小球质量为0.2kg;摆线长度为1m
(3)解:由F= ![]() ﹣mg知:图线的斜率值为:
﹣mg知:图线的斜率值为: ![]() =2N/J,因此对应状态b,Fb=4.0N,可求出小球在最高点的动能:
=2N/J,因此对应状态b,Fb=4.0N,可求出小球在最高点的动能: ![]() =
= ![]() ,于是得到:EKb=3.0J
,于是得到:EKb=3.0J
对小球从状态a到状态b的过程,有:W=EKb﹣EK=3.0﹣1.0=2.0J,
即:外界对系统做的功为2.0J.
答:外界对此系统做的功为2.0J
(4)解:在停止能量输入之后,小球在重力和轻绳拉力作用下在竖直面内做圆周运动,运动过程中机械能守恒.当小球运动到最低点时,绳中拉力达到最大值.
设小球在最低点的速度为v,对从b状态开始至达到最低点的过程应用机械能守恒定律,有:mg2l= ![]() mv2﹣EKb;
mv2﹣EKb;
设在最低点绳中拉力为Fm,由牛顿第二定律有:Fm﹣mg=m ![]() ,
,
两式联立解得:Fm=16N,
即:绷断瞬间绳中拉力的大小为16N
答:绷断瞬间绳中拉力的大小为16N
【解析】(1)在最高点,由牛顿第二定律可求小球能做完整的圆周运动满足的条件;(2)在最高点,由牛顿第二定律并结合图象信息可求小球质量和摆线长度;(3)由图象得斜率,根据动能定理求外界对系统做的功;(4)应用机械能守恒定律和牛顿第二定律求绷断瞬间绳中拉力的大小.
【考点精析】掌握向心力和机械能综合应用是解答本题的根本,需要知道向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力;系统初态的总机械能E 1 等于末态的总机械能E 2 ,即E1 =E2;系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ,即ΔE P减 =ΔE K增;若系统只有A、

 名校课堂系列答案
名校课堂系列答案