题目内容
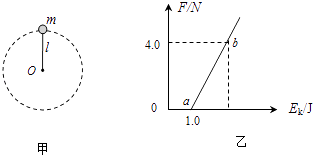
【题目】(14分)为了研究过山车的原理,某兴趣小组提出了下列设想:取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除 AB 段以外都是光滑的。其AB 与BC 轨道以微小圆弧相接,如图所示.一个小物块以初速度![]() =4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿 AB 方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数 μ = 0.50.(g=10 m/s2、sin37°= 0.60、cos37° =0.80)
=4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿 AB 方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数 μ = 0.50.(g=10 m/s2、sin37°= 0.60、cos37° =0.80)
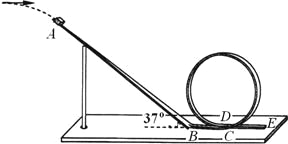
(1)求小物块到达A点时速度。
(2)要使小物块不离开轨道,并从轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件?
(3)为了让小物块不离开轨道,并且能够滑回倾斜轨道 AB,则竖直圆轨道的半径应该满足什么条件?
【答案】⑴vA=" 5" m/s⑵R1≤ 0.66m⑶R2≥ 1.65m
【解析】试题分析:(1)小物块做平抛运动,经时间 t 到达A处时,令下落的高度为h,水平分速度v0,竖直速度为vy,小物块恰好沿斜面AB方向滑下,则![]()
得vy =" 3" m/s,
所以小物块到A点的速度为5m/s
(2)物体落在斜面上后,受到斜面的摩擦力 f = μFN= μmgcos37°
设物块进入圆轨道到达最高点时有最小速度v1,此时物块受到的重力恰好提供向心力,令此时的半径为 R0,
则![]()
物块从抛出到圆轨道最高点的过程中,根据动能定理有:
mg(h + lsin37°–2R0)–μmgcos37°·l =![]() mv12–
mv12–![]() mv02.
mv02.
联立上式,解得R0=0.66m
若物块从水平轨道DE滑出,圆弧轨道的半径满足 R1≤ 0.66m
(3)为了让小物块不离开轨道,并且能够滑回倾斜轨道 AB,则物块上升的高度须小于或等于某个值R,则 mg(h + lsin37°) – μmgcos37°·l – mgR =" 0" –![]() mv02
mv02
解得R = 1.65m
物块能够滑回倾斜轨道 AB,则 R2≥ 1.65m

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案