题目内容
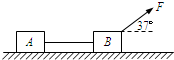 如图所示,质量为m=10kg的两个完全相同的物块A、B,它们之间用轻绳连接,作用在物块B上的恒定拉力F其方向与水平成θ=37°角斜向上、大小为100N,两物块以v=4.0m/s的速度沿水平面向右做匀速直线运动.(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
如图所示,质量为m=10kg的两个完全相同的物块A、B,它们之间用轻绳连接,作用在物块B上的恒定拉力F其方向与水平成θ=37°角斜向上、大小为100N,两物块以v=4.0m/s的速度沿水平面向右做匀速直线运动.(g取10m/s2,sin37°=0.6,cos37°=0.8)求:(1)物块与地面之间的动摩擦因数;
(2)若某时刻剪断轻绳,则剪断绳后物块A在水平地面上滑行的距离;
(3)从剪断轻绳到物块A停止运动的过程中,物块B受到的拉力冲量的大小.
分析:根据题意先将两物块作为整体,对其受力分析:受到重力mg、拉力F、地面的支持力和滑动摩擦力作用,根据力平衡条件和滑动摩擦力公式求出动摩擦力.当剪断轻绳后物块A在水平地面上受到滑动摩擦力作用而做匀减速运动滑行,要根据牛顿第二定律求出加速度,再位移公式求出位移
求出A运动的时间,根据I=Ft求出拉力冲量.
求出A运动的时间,根据I=Ft求出拉力冲量.
解答:解:(1)设两物体与地面间的动摩擦因素为μ,根据滑动摩擦力公式和平衡条件,
对A、B整体有:μmg+μ(mg-Fsinθ)=Fcosθ①
剪断轻绳以后,设物体A在水平地面上滑行的距离为s,有
μmg=ma②
v02=2as③
联解方程,代入数据得:
μ=0.57
s=1.4m
(3)A物体剪断轻绳以后运动的时间t=
=
=0.7s
所以拉力的冲量I=Ft=70Ns
答:(1)物块与地面之间的动摩擦因数为0.57;
(2)剪断绳后物块A在水平地面上滑行的距离为1.4m;
(3)从剪断轻绳到物块A停止运动的过程中,物块B受到的拉力冲量的大小为70Ns
对A、B整体有:μmg+μ(mg-Fsinθ)=Fcosθ①
剪断轻绳以后,设物体A在水平地面上滑行的距离为s,有
μmg=ma②
v02=2as③
联解方程,代入数据得:
μ=0.57
s=1.4m
(3)A物体剪断轻绳以后运动的时间t=
| v0 |
| a |
| 4 |
| 5.7 |
所以拉力的冲量I=Ft=70Ns
答:(1)物块与地面之间的动摩擦因数为0.57;
(2)剪断绳后物块A在水平地面上滑行的距离为1.4m;
(3)从剪断轻绳到物块A停止运动的过程中,物块B受到的拉力冲量的大小为70Ns
点评:本题是牛顿第二定律和力平衡条件的简单综合,要防止产生这样的错误解答:在拉力F作用时f=μmg.

练习册系列答案
相关题目
 如图所示,质量为m的球,被长为L的细绳吊起处于静止状态.现对小球施加水平向右的恒力F,小球开始向右运动,当细绳与竖直方向的夹角为60°,小球速度恰好为0( )
如图所示,质量为m的球,被长为L的细绳吊起处于静止状态.现对小球施加水平向右的恒力F,小球开始向右运动,当细绳与竖直方向的夹角为60°,小球速度恰好为0( )

 (2010?黑龙江模拟)(按题目要求作答,写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不得分)
(2010?黑龙江模拟)(按题目要求作答,写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不得分) (2005?青浦区模拟)如图所示,质量为m的带电金属小球,用绝缘细线与质量为M(M=2m)的不带电木球相连,两球恰能在竖直向上的足够大且场强为E的匀强电场中,以速度v匀速竖直向上运动,当木球升至a点时,细线突然断裂,木球升至b点时速度为零.则木球速度为零时,金属球的速度大小为
(2005?青浦区模拟)如图所示,质量为m的带电金属小球,用绝缘细线与质量为M(M=2m)的不带电木球相连,两球恰能在竖直向上的足够大且场强为E的匀强电场中,以速度v匀速竖直向上运动,当木球升至a点时,细线突然断裂,木球升至b点时速度为零.则木球速度为零时,金属球的速度大小为 (2003?徐州一模)如图所示,质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下,欲使木板静止在斜面上,木板上质量为m的人应以多大的加速度向下奔跑?
(2003?徐州一模)如图所示,质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下,欲使木板静止在斜面上,木板上质量为m的人应以多大的加速度向下奔跑?