题目内容
（2005?青浦区模拟）如图所示，质量为m的带电金属小球，用绝缘细线与质量为M（M=2m）的不带电木球相连，两球恰能在竖直向上的足够大且场强为E的匀强电场中，以速度v匀速竖直向上运动，当木球升至a点时，细线突然断裂，木球升至b点时速度为零．则木球速度为零时，金属球的速度大小为3v
3v
，a、b之间的电势差为| Ev2 |
| 2g |
| Ev2 |
| 2g |
分析：M与m组成的系统以速度v匀速竖直向上运动，说明它们的合力为0，故动量守恒；木球从a到b，只有重力做功，机械能守恒，从而求出木球上升的高度．
解答：解：（1）M与m组成的系统以速度v匀速竖直向上运动，说明它们的合力为0，故动量守恒：（M+m）v=mv′+M?0
代人数据求得：v′=3v
（2）木球从a到b，只有重力做功，所以-mgh=0-
mv2
整理得：h=
a、b之间的电势差：Uab=E?h=
故答案为：3V，
．
代人数据求得：v′=3v
（2）木球从a到b，只有重力做功，所以-mgh=0-
| 1 |
| 2 |
整理得：h=
| v2 |
| 2g |
a、b之间的电势差：Uab=E?h=
| Ev2 |
| 2g |
故答案为：3V，
| Ev2 |
| 2g |
点评：该题能够根据以速度v匀速竖直向上运动判断出M与m组成的系统动量守恒是解题的关键．属于简单题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
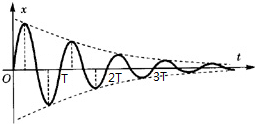（2005?青浦区模拟）弹簧振子可以作简谐振动，考虑阻力存在，振子振动过程中能量不断损失，这种振动称阻尼振动．现通过实验手段得到某振子阻尼振动的图象和经理论推导得到阻尼振动的周期公式 T=2π/（ω02-β2）1/2，观察图象后指出阻尼振动的特点