题目内容
18.人类第一次登上月球时,宇航员在月球表面做了一个实验:将一片羽毛和一个铁锤从同一个高度由静止同时释放,二者几乎同时落地.若羽毛和铁锤是从高度为h处下落,经时间t落到月球表面.已知引力常量为G,月球的半径为R,不考虑月球自转.求(1)求月球表面的自由落体加速度大小g月;
(2)月球的质量M;
(3)月球的“第一宇宙速度”大小v.
分析 (1)根据自由落体的位移时间规律可以直接求出月球表面的重力加速度;
(2)根据月球表面重力和万有引力相等,利用求出的重力加速度和月球半径可以求出月球的质量M;
(3)飞行器近月飞行时,飞行器所受月球万有引力提供月球的向心力,从而求出“第一宇宙速度”大小.
解答 解:(1)月球表面附近的物体做自由落体运动 h=$\frac{1}{2}$g月t2
月球表面的自由落体加速度大小 g月=$\frac{2h}{{t}^{2}}$
(2)若不考虑月球自转的影响 G$\frac{Mm}{{R}^{2}}$=mg月
月球的质量 M=$\frac{2h{R}^{2}}{G{t}^{2}}$
(3)质量为m′的飞行器在月球表面附近绕月球做匀速圆周运动m′g月=m′$\frac{{v}^{2}}{R}$
月球的“第一宇宙速度”大小 v=$\sqrt{{g}_{月}R}$=$\sqrt{\frac{2hR}{{t}^{2}}}$
答:(1)求月球表面的自由落体加速度大小为$\frac{2h}{{t}^{2}}$;
(2)a.月球的质量为$\frac{2h{R}^{2}}{G{t}^{2}}$;
(3)月球的“第一宇宙速度”大小为$\sqrt{\frac{2hR}{{t}^{2}}}$.
点评 结合自由落体运动规律求月球表面的重力加速度,根据万有引力与重力相等和万有引力提供圆周运动向心力求解中心天体质量和近月飞行的速度v.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
6.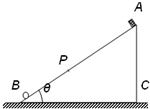 如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )
如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )
 如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )
如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )| A. | 水平地面对斜面体没有静摩擦作用力 | |
| B. | 小物块的电势能先增大后减小 | |
| C. | 小物块所受到的合外力一直减小 | |
| D. | 小物块损失的机械能大于增加的电势能 |
13.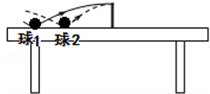 如图所示,相同的乒乓球1、2落台后恰好在等高处水平越过竖直球网,过网时的速度方向均垂直于球网.不计乒乓球的旋转和空气阻力,乒乓球自起跳到最高点的过程中,下列说法中正确的是( )
如图所示,相同的乒乓球1、2落台后恰好在等高处水平越过竖直球网,过网时的速度方向均垂直于球网.不计乒乓球的旋转和空气阻力,乒乓球自起跳到最高点的过程中,下列说法中正确的是( )
 如图所示,相同的乒乓球1、2落台后恰好在等高处水平越过竖直球网,过网时的速度方向均垂直于球网.不计乒乓球的旋转和空气阻力,乒乓球自起跳到最高点的过程中,下列说法中正确的是( )
如图所示,相同的乒乓球1、2落台后恰好在等高处水平越过竖直球网,过网时的速度方向均垂直于球网.不计乒乓球的旋转和空气阻力,乒乓球自起跳到最高点的过程中,下列说法中正确的是( )| A. | 起跳时,球1的速率大于球2的速率 | |
| B. | 球1的速度变化率小于球2的速度变化率 | |
| C. | 球1的飞行时间大于球2的飞行时间 | |
| D. | 过网时球1的速度等于球2的速度 |


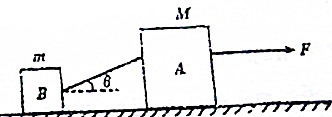 如图所示,在水平上放A、B两物体,质量分别为M和m,且M>m,它们与地面的动摩擦因数为μA、μB,且μA>μB,用一细绳连接,绳与水平方向成θ角,在A物体上加一水平拉力,使它们做匀速直线运动,细绳在物体A上的连接点可以上下移动调节,使得θ的大小可以在0°≤θ<90°的范围内变化,重力加速度为g,求:
如图所示,在水平上放A、B两物体,质量分别为M和m,且M>m,它们与地面的动摩擦因数为μA、μB,且μA>μB,用一细绳连接,绳与水平方向成θ角,在A物体上加一水平拉力,使它们做匀速直线运动,细绳在物体A上的连接点可以上下移动调节,使得θ的大小可以在0°≤θ<90°的范围内变化,重力加速度为g,求: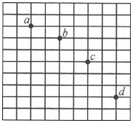 在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动途中的几个位置如图a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gl}$(用L、g表示),其值是0.7m/s (取g=9.8m/s2)
在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动途中的几个位置如图a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gl}$(用L、g表示),其值是0.7m/s (取g=9.8m/s2)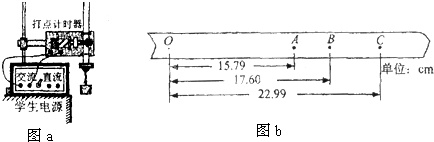
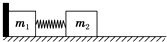 如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求:
如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求: