题目内容
9.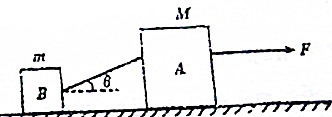 如图所示,在水平上放A、B两物体,质量分别为M和m,且M>m,它们与地面的动摩擦因数为μA、μB,且μA>μB,用一细绳连接,绳与水平方向成θ角,在A物体上加一水平拉力,使它们做匀速直线运动,细绳在物体A上的连接点可以上下移动调节,使得θ的大小可以在0°≤θ<90°的范围内变化,重力加速度为g,求:
如图所示,在水平上放A、B两物体,质量分别为M和m,且M>m,它们与地面的动摩擦因数为μA、μB,且μA>μB,用一细绳连接,绳与水平方向成θ角,在A物体上加一水平拉力,使它们做匀速直线运动,细绳在物体A上的连接点可以上下移动调节,使得θ的大小可以在0°≤θ<90°的范围内变化,重力加速度为g,求:(1)水平拉力F的最小值;
(2)绳中张力T的最小值.
分析 对整体分析,根据共点力平衡求出水平拉力的最小值.隔离对B分析,结合共点力平衡求出绳中的最小张力大小.
解答 解:(1)对整体,受力情况如图,根据平衡条件得 :F=fA+fB
:F=fA+fB
又fA=μA(mAg+Tsinθ),fB=μB(mBg-Tsinθ)
联立得到:
F=μA(mAg+Tsinθ)+μB(mBg-Tsinθ)=μAMg+μBmg+(μA-μB)Tsinθ
μA>μB,θ越大,F越大,可知当θ=0°时,拉力F最小,
所以最小拉力F=μAMg+μBmg.
(2)隔离对B分析,在水平方向上有:Tcosθ=fB,
在竖直方向上有:NB+Tsinθ=mg,
fB=μBNB,
解得T=$\frac{{μ}_{B}mg}{cosθ+{μ}_{B}sinθ}$=$\frac{{μ}_{B}mg}{\sqrt{1+{{μ}_{B}}^{2}}sin(θ+φ)}$,
可知T的最小值为$T=\frac{{μ}_{B}mg}{\sqrt{1+{{μ}_{B}}^{2}}}$.
答:(1)水平拉力F的最小值为μAMg+μBmg;
(2)绳中张力T的最小值为$\frac{{μ}_{B}mg}{\sqrt{1+{{μ}_{B}}^{2}}}$.
点评 本题考查了共点力平衡的综合运用,掌握整体法和隔离法的灵活运用,本题对数学能力要求较高,需加强这方面的训练.

练习册系列答案
相关题目
4.理想变压器原、副线圈的匝数比为4:1,原线圈接在u=220$\sqrt{2}$sin100πt V的交流电源上,副线圈所接的负载电阻是11Ω,则副线圈中电流大小是( )
| A. | 5A | B. | 11A | C. | 20A | D. | 55A |
14.某学习小组在学完“测定金属丝电阻率”实验后,想利用下列器材测定自来水的电阻率:

(1)用毫米刻度尺测量如图1所示的一段自来水管上两接线柱间距离为L; 用游标卡尺测量水管内径为d;
(2)用多用电表测量两接线柱间装满自来水电阻约20kΩ;为提高实验结果的准确程度,电流表应选用A1,电压表应选用V2(以上均填器材代号);
(3)为了达到上述目的,某同学设计出正确的电路原理图,并按电路图连接好实物图,如图2所示.接通电路后,当调节滑动变阻器的滑片时,发现电压表、电流表有示数但几乎不变,请指出哪一根导线发生了断路?c(只填写图中导线字母代号);
(4)若实验电路中电流表示数为I,电压表示数为U,可求得自来水的电阻率ρ=$\frac{{πd}_{\;}^{2}U}{4IL}$.(用以上测得的物理量符号表示)
| 器材(代号) | 规格 |
| 电流表(A1) | 量程0~1mA,内阻约为50Ω |
| 电流表(A2) | 量程0~0.6A,内阻约为0.1Ω |
| 电压表(V1) | 量程0~3V,内阻约为10kΩ |
| 电压表(V2) | 量程0~15V,内阻约为50kΩ |
| 滑动变阻器(R) | 阻值范围0~50Ω, 允许最大电流0.5A |
| 直流电源(E) | 输出电压15V,内阻不计 |
| 开关(S)、导线若干 | |
| 毫米刻度尺、游标卡尺 | |
| 多用电表 | |
| 一节两端可封 住的绝缘PVC水管 |

(1)用毫米刻度尺测量如图1所示的一段自来水管上两接线柱间距离为L; 用游标卡尺测量水管内径为d;
(2)用多用电表测量两接线柱间装满自来水电阻约20kΩ;为提高实验结果的准确程度,电流表应选用A1,电压表应选用V2(以上均填器材代号);
(3)为了达到上述目的,某同学设计出正确的电路原理图,并按电路图连接好实物图,如图2所示.接通电路后,当调节滑动变阻器的滑片时,发现电压表、电流表有示数但几乎不变,请指出哪一根导线发生了断路?c(只填写图中导线字母代号);
(4)若实验电路中电流表示数为I,电压表示数为U,可求得自来水的电阻率ρ=$\frac{{πd}_{\;}^{2}U}{4IL}$.(用以上测得的物理量符号表示)
1.如图所示,理想变压器的输入电压U恒定,在下列措施中能使电流表示数变小的是( )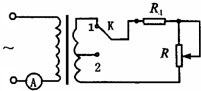

| A. | 保持变阻器的滑片不动,将K从2拨向1 | |
| B. | 保持变阻器的滑片不动,将K从1拨向2 | |
| C. | 保持K与1相连接,将变阻器的滑片向上移 | |
| D. | 保持K与2相连接,将变阻器的滑片向上移 |
 如图所示,在x轴下方的区域内存在沿y轴负方向的匀强电场,电场强度为E,在x轴上方有半径为R的圆形区域内存在匀强磁场,磁场的方向垂直于xy平面并指向纸面内,磁感应强度为B.y轴下方的A点与O点的距离为d,一质量为m、电荷量为q的带负电粒子从A点由静止释放,经电场加速后从O点射入磁场,不计粒子的重力作用.
如图所示,在x轴下方的区域内存在沿y轴负方向的匀强电场,电场强度为E,在x轴上方有半径为R的圆形区域内存在匀强磁场,磁场的方向垂直于xy平面并指向纸面内,磁感应强度为B.y轴下方的A点与O点的距离为d,一质量为m、电荷量为q的带负电粒子从A点由静止释放,经电场加速后从O点射入磁场,不计粒子的重力作用.
 如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )
如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )