题目内容
7.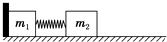 如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求:
如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求:①当弹簧拉伸到最长时,木块m1的速度多大?
②在以后的运动过程中,木块m1速度的最大值为多少?
分析 ①先研究木块m2向左压缩弹簧到弹簧第一次恢复原长的过程,根据机械能守恒可得到此时木块m2的速度为v0=0.2m/s.此后,弹簧开始伸长,当弹簧拉伸最长时,木块m1、m2速度相同,设为v,由动量守恒定律可求得v.
②当弹簧再次恢复到原长时,m1获得最大速度,再对弹簧和两个木块组成的系统动量守恒和机械能守恒列方程,求解木块m1速度的最大值.
解答 解:①木块m2弹回后,在弹簧第一次恢复原长时带动m1运动,
设此时木块m2的速度为v0,由机械能守恒定律可知:v0=2m/s,
当弹簧拉伸最长时,木块m1、m2速度相同,设为v,规定向左为正方向,
由动量守恒定律得:m2v0=(m1+m2)v,解得:v=1.5m/s,
②当弹簧再次恢复到原长时,m1获得最大速度为v1,此时m2的速度为v2,
规定向右为正方向,由动量守恒定律得:m2v0=m1v1+m2v2,
由机械能守恒定律得:$\frac{1}{2}$m2v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22,
解得:v1=3m/s v2=1m/s,(v1=0m/s v2=2m/s 不合题意,舍去);
答:①当弹簧拉伸到最长时,木块m1的速度是1.5m/s.
②在以后的运动过程中,木块m1速度的最大值为3m/s.
点评 解决本题首先要明确研究的过程,其次把握信隐含的条件:弹簧伸长最长时两木块的速度相同.考查学生应用动量守恒定律和能量守恒定律解决物理问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.用m表示人造地球同步卫星的质量,h表示它离地面的高度,R0表示地球半径,g0表示地球表面处的重力加速度,ω0表示地球自转的角速度,则通讯卫星所受地球对它的万有引力大小是( )
| A. | 0 | B. | $\root{3}{{R}_{0}^{2}{g}_{0}{ω}_{0}^{4}}$ | C. | $\frac{m{R}_{0}^{2}{g}_{0}}{({R}_{0}+h)^{2}}$ | D. | mg0 |
12. 如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1J,若A点电势为-10V,则( )
如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1J,若A点电势为-10V,则( )
 如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1J,若A点电势为-10V,则( )
如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1J,若A点电势为-10V,则( )| A. | B点电势为零 | B. | 电场线方向向左 | ||
| C. | 电荷运动的轨迹可能是图中曲线a | D. | 电荷运动的轨迹可能是图中曲线b |
19. 如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )
如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )
 如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )
如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )| A. | 14m/s | B. | 3.5m/s | C. | 2m/s | D. | 1m/s |
17. 如图所示,R1为定值电阻,R2是正温度系数的金属热电阻(即温度越高,电阻值越大),L为小灯泡,当温度下降时( )
如图所示,R1为定值电阻,R2是正温度系数的金属热电阻(即温度越高,电阻值越大),L为小灯泡,当温度下降时( )
 如图所示,R1为定值电阻,R2是正温度系数的金属热电阻(即温度越高,电阻值越大),L为小灯泡,当温度下降时( )
如图所示,R1为定值电阻,R2是正温度系数的金属热电阻(即温度越高,电阻值越大),L为小灯泡,当温度下降时( )| A. | 电流表的示数增大 | B. | R2两端的电压增大 | ||
| C. | 小灯泡变亮 | D. | 小灯泡变暗 |
 如图所示,一簇平行线为未知方向的匀强电场的电场线,沿与此平行线成60°角的方向,把1C的负电荷从A点移到B点,电场力 做功为2J,A、B间距为2cm 求:
如图所示,一簇平行线为未知方向的匀强电场的电场线,沿与此平行线成60°角的方向,把1C的负电荷从A点移到B点,电场力 做功为2J,A、B间距为2cm 求: 如图所示,为使带负电的点电荷q在一匀强电场中沿直线匀速地由A点运动到B点,必须对该电荷施加一个恒力F,如图所示.若AB=20cm,α=37°,q=-3×10-7C,F=1.2×10-4k,A点的电势ΦA=100V(不计负电荷的重力),求:
如图所示,为使带负电的点电荷q在一匀强电场中沿直线匀速地由A点运动到B点,必须对该电荷施加一个恒力F,如图所示.若AB=20cm,α=37°,q=-3×10-7C,F=1.2×10-4k,A点的电势ΦA=100V(不计负电荷的重力),求: