题目内容
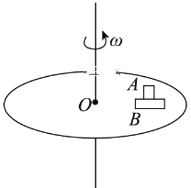
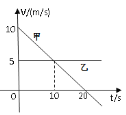
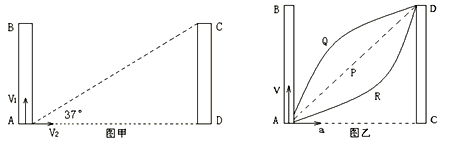
【题目】足够长的光滑水平面上，有10个相同的小球沿直线等间隔均匀分布，总长度为l，并以相同的速度v0向右运动，如图甲所示。在小球的正前方有一“加速带”AB，当小球从左端A进入加速带后在水平恒力作用下被加速，直至从右端B离开，小球经过加速带前后速度的变化情况如图乙所示。已知1号球刚从B端离开时，4号球刚好从A端进入。不考虑球的大小，试求
(1)10个小球最终分布的总长度。
(2)加速带对10个小球做功的总功率P。已知小球在加速带上所受水平恒力为F。
【答案】(1)
(2) 
【解析】
（1）已知1号球刚从B端离开时，4号球刚好从A端进入，因此1、4号两球的运动时间有一定的关系；在运动示意图中补画出1号球刚从A端进入时，2、3、4号球的位置关系；结合题中条件求出此时4号球与1号球之间的距离，根据题意和图示，利用“等时性”，把1号球在加速带上运动的时间转化为4号球做匀速运动所用的时间。小球离开加速带后以3v0 做匀速运动；已知1号球刚从B端离开时，4号球刚好从A端进入，在运动示意图中补画出4号球刚从B端离开时，1、2、3号球的位置关系；利用“等时性”，把1号球在右侧做匀速运动的时间转化为4号球在加速带上运动的时间，从而可以求出4号球刚从B端离开时1、4号两球之间的距离，推算出小球离开加速带后相邻小球的间隔距离，则最终10个小球分布的总长度L等于9个间隔距离。
（2）已知小球在加速带上运动的平均速度为2v0，且求出了小球在加速带上运动的时间T，据此可求出加速带的长度；已知物体加速带上受到的水平恒力为F，可求出加速带对10个小球所做的总功；补画出10号球的运动示意图，根据题意和图示可知，加速带对10个小球的做功时间等于1号球刚从A端进入到10号球刚从B端离开所用的时间，再把该时间转化为10号球运动的总时间；最后根据功率公式求出加速带对10个小球做功的总功率P。
（1）“最终”是指10个小球全部离开了加速带。根据图乙可知，所有小球从加速带B端出来后速度都被加速到了3v0，且保持这个速度不变，这就意味着一旦10个小球全部从B端出来后，它们的总长度也会保持不变。这个长度就是10号球刚离开B端时，它与1号间的距离。
由于每个小球在加速带上运动的情况完全相同，因此，小球依次从B 端离开加速带的时间差等于依次进入加速带的时间差。这样，10号球与1号球出加速带的时间差与进入加速带的时间差Δt相等，而
故10号球刚从B端出来时，1号与10号间的距离L=3v0Δt
解得L=3l
此即10个小球最终分布的总长度。
（2）因加速带对10个小球做功并不同步，故对10个小球做功的总功率要小于对单个小球做功的功率之和。
小球在加速带上运动的时间
小球在加速带上运动的平均速度
故加速带长度为
因而加速带对10个小球所做总功为W=10FL0
加速带做功的总时间应是从1号球进入加速带A端开始，直到10号球离开加速带B端为止，这段时间即t=Δt +T
又加速带对10个小球做功的总功率为
解得P=5Fv0
