题目内容
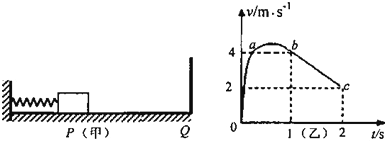
【题目】如图甲所示,在粗糙的水平面上,一质量m=0.1kg可视为质点的滑块压缩一轻弹簧并被锁定,滑块与弹簧不相连,解除锁定前滑块处于P处,t=0时解除锁定计算机通过传感器描绘出滑块的速度时间图象如图乙所示,其中oab段为曲线,bc段为直线,在t1=1s时滑块已经在水平面上滑行s=4m的距离.在滑块运动方向上与P相距7m的Q处有一竖直挡板,若滑块与挡板碰撞被弹回时无能量损失,g取10m/s2,求:
(1)滑块与水平面间动摩擦因数μ;
(2)锁定时弹簧具有的弹性势能Ep;
(3)滑块停下时与挡板的距离.
【答案】(1)滑块与地面的动摩擦因数为0.2;
(2)锁定时弹簧具有的弹性势能是1.6J;
(3)滑块停下时与挡板的距离是1m.
【解析】
试题1.从速度时间﹣﹣图象得到滑块脱离弹簧后减速滑行时的加速度,然后根据牛顿第二定律列式求解动摩擦因数;
2.对全过程运用动能定理,求出弹簧弹力做的功,从而得出弹性势能的最大值.
3.合力为零时,即加速度为零时速度最大,根据平衡方程求得弹簧的形变量,从而求得前进的距离.
解:(1)从图象可知,滑块脱离弹簧后的加速度为:
![]() m/s2
m/s2
由牛顿第二定律有:﹣μmg=﹣ma1
得:μ=0.2
(2)t1=1s时滑块已经在水平面上滑行s=4m的距离;设弹簧对滑块做功为W,由动能定理知:
W﹣μmgs=![]() m
m![]()
代入数据得:W=1.6J
由图可知此时弹簧已经恢复原长,弹性势能已经全部释放,所以 弹性势能Ep:EP=W=1.6J
(3)弹簧在恢复原长后只有摩擦力做功,由动能定理得:
![]()
代入数据得:x=4m
所以滑块停下时与挡板的距离为:
s=4m+4m﹣7m=1m
答:(1)滑块与地面的动摩擦因数为0.2;
(2)锁定时弹簧具有的弹性势能是1.6J;
(3)滑块停下时与挡板的距离是1m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目