题目内容
设地球的质量为M，绕太阳做匀速圆周运动，有一质量为m的飞船，由静止开始自P点在恒力F的作用下，沿PD方向做匀加速直线运动.若一年后飞船在D点掠过地球上空，且再过两个月又在Q处掠过地球上空，如图所示，根据以上条件，求地球与太阳间的万有引力的大小.（忽略飞船受地球和太阳的万有引力作用的影响）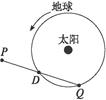
F=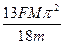
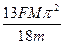
设地球公转周期为T，则两个月时间为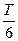
，两个月时间地球绕太阳转过60°角.
设地球公转半径为R，则由几何关系得：
DQ="R " PD=
aT2
PQ=a(
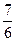T)2
F=ma
PQ=PD+DQ
解得：R=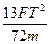
所以地球与太阳间的万有引力为：
F=M
R=.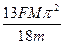
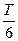，两个月时间地球绕太阳转过60°角.设地球公转半径为R，则由几何关系得：
DQ="R " PD=
aT2PQ=
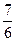a(T)2F=ma
PQ=PD+DQ
解得：R=
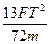
所以地球与太阳间的万有引力为：
F=M
R=.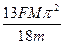
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
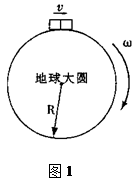
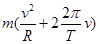
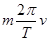
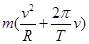
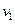R/T的圆周运动）时，火车对轨道的压力为N；在此基础上，又考虑到这列火车匀速相对地面又附加了一个线速度v做更快的圆周运动，并设此时火车对轨道的压力为N/，那么单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量（N－N/）为 （ ）
，加速度为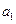
，地球赤道上的物体随地球自转的向心加速度为
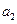，第一宇宙速度为
，地球半径为R。则下列关系式正确的是（）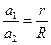
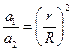
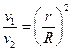
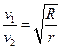
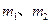，相距为L，试求；
、
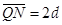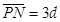，离子重力不计。