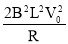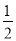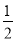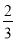题目内容
(19分)如图所示,在匀强电场中建立直角坐标系xOy,y轴竖直向上,一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线运动,重力加速度为g。
(1)求匀强电场场强E;
(2)若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点,M、N两点关于原点O对称,距离为L,微粒运动轨迹也关于y轴对称。已知磁场的磁感应强度大小为B,方向垂直xOy平面向外,求磁场区域的最小面积S及微粒从M运动到N的时间t。

(1) 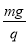 ;方向:竖直向上 (2)
;方向:竖直向上 (2) 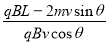 +
+ 
【解析】
试题分析:(1)对微粒有qE-mg = 0 (2分) 得E = 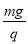 (1分) 方向:竖直向上 (1分)
(1分) 方向:竖直向上 (1分)
(2)微粒在磁场中有qvB=m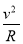 (2分) 得R =
(2分) 得R = 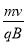 (1分)
(1分)
如图所示,当PQ为圆形磁场的直径时,圆形磁场面积最小。
有r=Rsinθ (3分)

其面积S=πr2 = 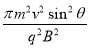 (2分)
(2分)
又T = 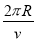 (或T =
(或T =  ) (1分)
) (1分)
根据几何关系可知偏转角为2θ (1分)
则在磁场中运动的时间t2 =  T =
T =  (1分)
(1分)
又 MP=QN= 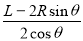 (1分)
(1分)
且有t1 = t3 = 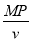 (1分)
(1分)
故运动的时间t = t1+t2+t3 = + = +
= + 
= 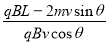 +
+  (2分)
(2分)
考点:带电粒子在匀强磁场中的运动.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目