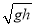Question

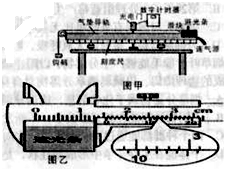
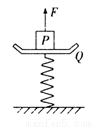
一个弹簧秤放在水平地面上，Q为与轻弹簧上端连在一起的秤盘，P为重物，已知P的质量M =10.5 kg，Q的质量 m =1.5 kg，弹簧的质量不计，劲度系数 k =800 N/m，系统处于静止.如图所示，现给P施加一个方向竖直向上的力F，使它从静止开始向上做匀加速运动，则在向上运动的过程中力F随时间变化的图象是（ ）

 

 

Answer 1

C

【解析】

试题分析: 最初时，弹簧的弹力等于PQ的总重力（M+m）g。

刚开始运动时，PQ的加速度相同，把PQ看成一个整体，PQ整体受到的外力共有3个：重力、向上的力F及弹簧弹力F弹，做匀加速运动，根据牛顿第二定律得：

F合=（M+m）a

F+F弹-（M+m）g=（M+m）a

设P的位移为x

所以F=（M+m）（a+g）-（（M+m）g-kx）=（M+m）a+ kat2/2；

即在P与Q分离前F随时间变化图象是抛物线，且t=0时，F=（M+m）a

当P与Q分离时，P只受重力和F作用，仍做匀加速运动，此时F为恒力．故C正确

考点：牛顿第二定律